MatinSAR
- 673
- 204
- Homework Statement
- Find partial derivatives
- Relevant Equations
- dy/dx=(dy/dt)(dt/dx)
Can someone please help me to find out what happened here ?
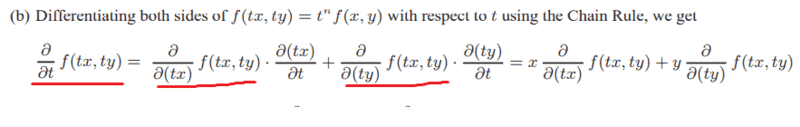
This discussion focuses on the manipulation of partial derivatives, specifically differentiating a function ##f## with respect to its arguments and subsequently with respect to time ##t##. The key formula presented is $$\partial f(u,v) / \partial t = (\partial f/ \partial u) (\partial u/ \partial t) + (\partial f/ \partial v) (\partial v/ \partial t)$$, where ##u = tx## and ##v = ty##. Participants clarified the confusion surrounding the term "tx" and confirmed the correct application of the chain rule in this context.
PREREQUISITESStudents and professionals in mathematics, physics, and engineering who are working with multivariable functions and need to understand the application of partial derivatives in various contexts.
That "tx" confused me ...ergospherical said:It's differentiating ##f## with respect to its arguments, then differentiating the arguments with respect to ##t##. It might be clearer if you write ##u = tx## and ##v=ty##, then
$$\partial f(u,v) / \partial t = (\partial f/ \partial u) (\partial u/ \partial t) + (\partial f/ \partial v) (\partial v/ \partial t)$$