Number of moles necessary to get piston back to initial position

[lorenz0]

Homework Statement

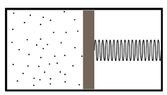
In a cylindrical piston of section S a piston can move without friction. A mole of ideal monoatomic gas is confined to the left, the right chamber is empty and contains a spring with elastic constant k which would be at rest if the piston were all the way to the left.
Initially the gas is at rest in an "A" state ($p_A = 10^5 Pa, V_A = 25 dm^3$). It takes place through an exchange of heat with the outside
a slow transformation until reaching a "B" state with volume
halved. Calculate :
a) the heat $Q$ exchanged by the gas with the external environment to complete the transformation,
b) the entropy change $\Delta S_G$ of the gas,
c) how many moles $n_{agg}$ of gas must be added to bring the piston back to the initial position assuming that the temperature remains that of state "B"?

Relevant Equations

$F_{spring}=-kx, \Delta U=Q-L, W=\int_{a}^{b} \vec{F}\cdot\vec{dx}, \Delta S=nC_V\ln(\frac{T_f}{T_i})+nR\ln(\frac{V_f}{V_i}), PV=nRT$

a) $T_A=\frac{p_AV_A}{nR}=300.7K, P_A V_A=kL^2=nRT_A$, $P_B S=k\frac{L}{2}\Rightarrow P_B V_B=k(\frac{L}{2})^2 \Rightarrow P_B=\frac{kL^2}{2V_A}=\frac{P_AV_A}{2V_A}=\frac{P_A}{2}$, $W_{spring\to gas}=\int_{L}^{L/2}kxdx=-\frac{3}{8}kL^2=-\frac{3}{8}nRT_A$$\Rightarrow Q=L+\Delta U=-\frac{3}{8}nRT_A+n\cdot\frac{3}{2}R (\frac{T_A}{4}-T_A)\simeq 3750 J$

b) $\Delta S_{gas}=nC_V\ln(\frac{T_f}{T_i})+nR\ln(\frac{V_f}{V_i})=nC_V\ln(\frac{T_A /4}{T_A})+nR\ln(\frac{V_A/2}{V_A})=-4nR\ln(2)=-23 J/K$

EDIT: I think I have managed to solve also part c)

c) $T_B=\frac{P_BV_B}{nR}=\frac{1}{nR}\cdot\frac{kL^2}{2V_A}\cdot\frac{V_A}{2}=\frac{1}{4}\frac{kL^2}{nR}=\frac{1}{4}\cdot\frac{P_AV_A}{nR}=\frac{1}{4}T_A$ so $n_f=\frac{P_AV_A}{RT_B}=\frac{10^5\cdot 25\cdot 10^{-3}}{8.314\cdot\frac{300.7}{4}}mol=4mol$ so $\Delta n=n_f-n_i=(4-1)mol=3mol$

 

[Chestermiller]

In part (a), your W is the work done by the gas on the springbecause $Q=W+\Delta U$. So, for Q, I get $$Q=-1.5RT_A=-3750\ J$$

The rest looks good. Very nice job.