@TSny
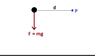
First I should say, when I said "accelerating axis of rotation" that is not really what I meant. I wasn't sure how to articulate myself (so I didn't try) but this is what I meant:
For the first instant we have a stationary axis somewhere, and then at a future instant we move the axis to somewhere else, but the axis is still stationary. So it's like it's instantaneously stationary, yet it's location is changing.
I'm still not sure if that makes sense... but that is what I've been imagining.
So in your example it's like we start the axis at the level of the particle, and then the particle falls a bit, and then we move the axis down a bit, but the axis is meant to be stationary at each instant.