Oh god Gauss-Jordan Elimination.

[Axmann]

1. Homework Statement :

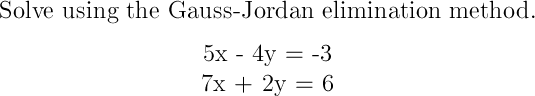
2. Relevant equations:

Not applicable.

3. The attempt at a solution:

This is where the problem begins. It's funny, because I used to be good
at matrices back in high school, but when I look at them now, I don't
understand why I keep getting different answers when I do different
elementary row operations. I know how to get my values in reduced
echelon form and such, but my problem is knowing which row operations
are "allowed". Any assistance on this?

 

[Axmann]

Oh, wait. Let me ask a quick question.

Can you add or subtract a single number to or from a single row? Or can you only multiply/divide rows, and only add-subtract rows from/to each other?

 

[the_kool_guy]

no we cannot add or subtract a single number from a row.
we can add multiples of other rows to a single row

 

[Mark44]

There are three operations:
1) Replace a row/equation by a nonzero multiple of itself. For example, you could multiply both sides of one row/equation by 2, say.
2) You can exchange (swap) two rows/equations.
3) You can add a nonzero multiple of one row/equation to another row/equation.

 

[Axmann]

There are three operations:
1) Replace a row/equation by a nonzero multiple of itself. For example, you could multiply both sides of one row/equation by 2, say.
2) You can exchange (swap) two rows/equations.
3) You can add a nonzero multiple of one row/equation to another row/equation.

Thank you! That definitely helps! I'm getting answers that actually make sense now.

So, can you divide both sides of a row by a nonzero number too, or only replace it with a nonzero multiple of itself?

 

[HallsofIvy]

I have no idea what you mean by "both sides of a row". However, "dividing by a number" is the same as "multiplying by the reciprocal of the number" so there is absolutely no difference between "divide both sides of a row by a nonzero number" and "replace it with a nonzero multiple of itself".