JackFyre
- 15
- 7
Is the below Displacement time graph posible?
if an object is in motion at a constant velocity, is it possible for it to stop instantaneously, or does there have to be a decelaration?
According to Newton's first, an object will remain in its state of constant velocity unless acted upon by external forces. Here, our object has a constant velocity, but then it stops; therefore, there has to be an external force. Now, if there IS an external force, there would be an acceleration, which would result in a curve in the S-T graph.
but there is no curve... So is that possible?
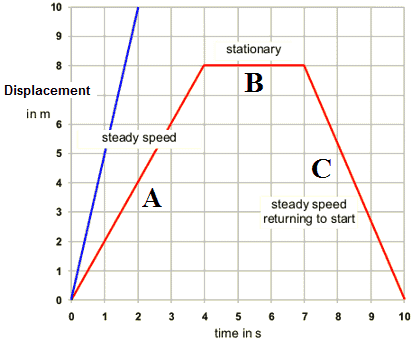
if an object is in motion at a constant velocity, is it possible for it to stop instantaneously, or does there have to be a decelaration?
According to Newton's first, an object will remain in its state of constant velocity unless acted upon by external forces. Here, our object has a constant velocity, but then it stops; therefore, there has to be an external force. Now, if there IS an external force, there would be an acceleration, which would result in a curve in the S-T graph.
but there is no curve... So is that possible?