On shell and off shell simultaneously?

[CAF123]

I am considering the following one loop virtual correction in the DIS process.

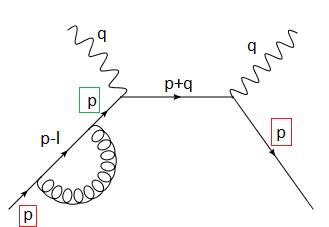
where I have a quark of momentum $p$ coming in, emitting a gluon before interacting with a photon of momentum $q$ to produce a fermionic propagator with momentum $p+q$. My question is, in the red box, I have an on shell initial or final state quark $p^2=0$ but in the green box I have an off shell fermionic quark propagator $p^2 \neq 0$.

So, in my equations, in particular upon evaluation of the loop integral $$\int d^D l \frac{\text{Tr}( \not p \gamma^{\nu} (\not p + \not q) \dots)}{p^2 (p+q)^2 (p-l)^2}$$ where the denominators are all off shell terms, in simplifying the numerator (the trace results in dot products of all the momenta scales in the problem) would I use $p^2=0$ or $p^2 \neq 0$?

 

[mfb]

p should be the same as p, I don't see how it could be off-shell if the gluon is connected as in the diagram.

 

[CAF123]

p should be the same as p, I don't see how it could be off-shell if the gluon is connected as in the diagram.

I should have maybe drawn it with a cut through the propagator p+q. I want to compute the hadronic tensor for this diagram which is the discontinuity of the forward scattering process I showed. Does that make more sense in the set up?

 

[RGevo]

This diagram, is the 1PI insertion onto the external leg.

Normally, the approach is to renormalise the wave functions in the on shell scheme.

In this set up, this diagram is canceled with that of the UV counterterm inserted onto this leg exactly.

In which case, you never need to calculate this diagram ever.

You would have to consider this gluon type attachment in the internal propagator. This would be off-shell, and would require the mass counterterm (the CT for a fermion propagator) to cancel the UV pole.