SUMMARY
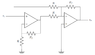
This discussion centers on the effective analysis of operational amplifier (op-amp) circuits, emphasizing the superiority of nodal analysis over basic gain formulas. Participants agree that while formulas like inverting gain (-Rf/Rin) and non-inverting gain (1 + Rf/Rin) are useful, they can lead to confusion in complex circuits. The consensus is to prioritize understanding nodal analysis, which simplifies the derivation of these formulas and ensures accuracy in circuit analysis. The discussion highlights the importance of recognizing node potentials, particularly between nodes D and E, which are identified as the same due to their shared voltage.
PREREQUISITES
- Understanding of operational amplifier configurations (inverting and non-inverting).
- Familiarity with nodal analysis techniques in circuit design.
- Knowledge of basic circuit laws, including Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL).
- Ability to apply gain formulas for op-amps in circuit analysis.
NEXT STEPS
- Study the principles of nodal analysis in greater detail.
- Practice deriving gain formulas for both inverting and non-inverting op-amps.
- Explore advanced op-amp configurations and their applications.
- Review examples of complex circuits that require nodal analysis for accurate evaluation.
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in analyzing or designing op-amp circuits will benefit from this discussion.