Waits
- 1
- 0
Thread moved from the technical forums to the schoolwork forums
Hello,
I am trying to solve a problem about an open Gas Turbine. The given information would be:
- An open gas turbine draws in air from the surroundings having the m, cp, T1 and constant kL with the next values:
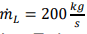 ,
,
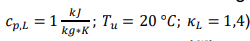 - The air flow is heat over natural gas supplied:
- The air flow is heat over natural gas supplied:
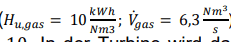 - The pressure ratio is 𝜋 = 10.
- The pressure ratio is 𝜋 = 10.
- In the turbine, the exhaust gas is brought to ambient pressure relaxed.
- For simplification it is assumed:
I should calculate T2, T3, T4 and efficiency.
But I am stuck at the temperatures calculation.
- I know T1=20º+273=293K.
- I know the relation:
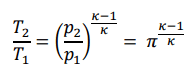 With this I can calculate T2=T1*(𝜋)^(k-1/k)=293K*(10)^(0.4/1.4)=565.783K
With this I can calculate T2=T1*(𝜋)^(k-1/k)=293K*(10)^(0.4/1.4)=565.783K
- But now, how can I calculate the p1 or p2, the pressures from T1/T2. If I get p1 or p2, then I can calculate through their relationships with 𝜋, the other pressure and go further to p3. I also been given the mair and cp, but not sure how I can relate this to the pressures.
Thank you very much in advance.
I am trying to solve a problem about an open Gas Turbine. The given information would be:
- An open gas turbine draws in air from the surroundings having the m, cp, T1 and constant kL with the next values:
- In the turbine, the exhaust gas is brought to ambient pressure relaxed.
- For simplification it is assumed:
Medium is an ideal gas.
The mass flow of the supplied natural gas can be neglected
become: 𝑚̇ 𝑧𝑢 = 𝑚̇ 𝑎𝑏 = 𝑚̇ 𝐿𝑢𝑓𝑡
The heat capacity of the exhaust gas corresponds to the heat capacity
of the air: 𝑐𝑝,𝑎𝑖𝑟 ≈ 𝑐𝑝,𝑎𝑏𝑔𝑎𝑠
The isentropic exponent is the same for all states valid.
The mass flow of the supplied natural gas can be neglected
become: 𝑚̇ 𝑧𝑢 = 𝑚̇ 𝑎𝑏 = 𝑚̇ 𝐿𝑢𝑓𝑡
The heat capacity of the exhaust gas corresponds to the heat capacity
of the air: 𝑐𝑝,𝑎𝑖𝑟 ≈ 𝑐𝑝,𝑎𝑏𝑔𝑎𝑠
The isentropic exponent is the same for all states valid.
I should calculate T2, T3, T4 and efficiency.
But I am stuck at the temperatures calculation.
- I know T1=20º+273=293K.
- I know the relation:
- But now, how can I calculate the p1 or p2, the pressures from T1/T2. If I get p1 or p2, then I can calculate through their relationships with 𝜋, the other pressure and go further to p3. I also been given the mair and cp, but not sure how I can relate this to the pressures.
Thank you very much in advance.