Operator for the local average of a growing oscillating function

[Swamp Thing]

TL;DR

How can we get the average value around a point of an oscillating function that has an increasing envelope?

First some background, then the actual question...
Background:
(a) Very simple example: if we take $Asin(x+ϕ)+0.1$, the average is obviously 0.1, which we can express as the integral over one period of the sine function. (assume that we know the period, but don't know the phase or other parameters of the function).

(b) More complicated example: Take $x^2 sin(x+\phi) + 0.1$

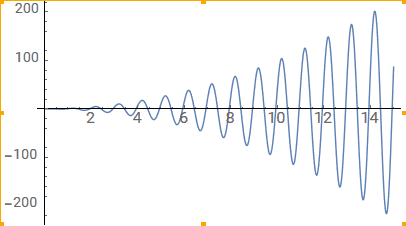Here simple integration won't help, because the integral depends on where in the cycle we start from. If we integrate a positive half-cycle first and then a negative half-cycle, we get a negative result, and vice versa. To avoid favoring either the positive or negative half cycles, we can multiply our function by a window function:

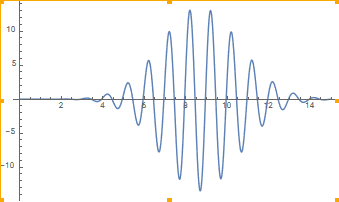And now if we integrate over the window we can retrieve the bias (average) of 0.1.

Question:
Can we have a more rigorous way of recovering the "0.1" that gives the same result as the windowing method? Something that involves a smart way of integrating over one cycle (or a whole number of cycles) in different ways, then combining them and calibrating out the growth (envelope) function? -- But without actually knowing the envelope function explicitly?

 

[Stephen Tashi]

To have hope of finding an average value, we'd have to know that the definition of such a value makes it unique.

So a basic question (which I cannot answer) is:

Let f(x) be a function such that f(x) = A(x) p(x) + k where A(x) is a non-periodic function, p(x) is periodic function and k is a constant. For some f(x), can there exist a different representation of f(x) as f(x) = B(x) q(x) + m where B(x) is a non-periodic function, q(x) is a periodic function and m is a constant different than k ?

For your examples, we can assume all the above functions are differentiable. The examples are also cases where A'(x) > 0, B'(x) > 0.

 

[Swamp Thing]

Useful perspective, thanks!