Optical pumping vs Rabi cycle - what is the difference between their conditions?

[JD23]

Optical pumping "is a process in which light is used to raise (or "pump") electrons from a lower energy level in an atom or molecule to a higher one".
In contrast, Rabi cycle "is the cyclic behavior of a two-level quantum system in the presence of an oscillatory driving field."

In the first we raise the number of excited atoms, in the second we have oscillations - different behaviors in looking similar conditions.
So what is the difference between conditions to get the first or the second?

E.g. shooting with continuous laser a two-state target in corresponding energy, should we just raise the number of excited atoms (to what N_1/N_0?), or should they oscillate?
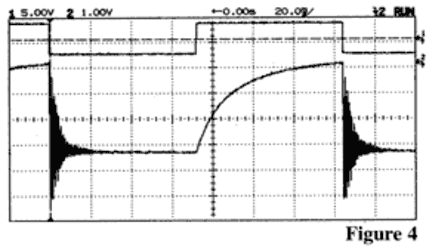
Here is some experiment: https://www.teachspin.com/optical-pumping - looks like raise then oscillate (?) - what exactly changes between these two regimes?

 

[Cthugha]

Optical pumping is a more general term. If you have a look at the definition of the Rabi frequency in optical systems, you will find that it includes the product of the electric dipole moment of the atom and the electric field used to drive it. So the field strength changes the Rabi frequency, the dipole moment changes the Rabi frequency and even the relative orientation of both changes it.

Accordingly, for a single two-level system, you will always end up with a well-defined Rabi frequency. For an ensemble of many two-level systems, things get more complicated. If you use a Gaussian beam, atoms at the center of the spot will see a different field strength compared to atoms located away from the center, so they will be subject to different Rabi frequencies. The dipole moments of the atoms may also be oriented randomly with respect to the electric field. In that case, all the atoms will also effectively be subject to different Rabi frequencies.

What you get effectively, is that each atom undergoes Rabi oscillations at its own frequency until some interaction destroys the coherent superposition and puts the atom either in the excited or the ground state. How often these interactions happen, depends on many things, e.g., the density of the atoms you look at.

Very loosely speaking and as a rule of thumb, one mostly talks about Rabi oscillations when investigating single two-level systems or several two-level systems which are "identical" enough to show only small deviations in their individual Rabi frequencies and which interact so little that one manages to introduce at least a full Rotation cycle on average before interactions destroy the superpositions. In individual fields or experiments, the terminology may vary.

 

[JD23]

Thank you, so shooting a two-level system with continuous laser of corresponding frequency, what will be evolution of population of excited atoms n_2 of this system?
Like in the previously attached diagram from https://www.teachspin.com/optical-pumping - first increase of n_2, and then oscillations?

In the first "pumping phase" it seems we can alternatively use the standard absorption equation from https://en.wikipedia.org/wiki/Einstein_coefficients#Photon_absorption: -dn_2/dt =

But then it would break - switch to "oscillation phase" due to decoherence of phases of the atoms in Rabi oscillation?

 

[Cthugha]

A two-level system does not really have a population of excited atoms because it is typically just one atom. But the probability to find it in the excited state will initially oscillate.

In the teachspin figure, it is the other way round compared to your description. First, there are oscillations and then n2 settles to an increased value. Figure 5 is a zoom in on the initial increase of figure 4 at a much better temporal resolution. The whole figure 5 covers about two boxes in figure 4.

Physically, what happens is the following: Initially, you are in the ground state. Then the light field introduces oscillations between the ground and the excited state. Some interactions will then probabilistically put the atom in the ground or the excited state depending on which part of the oscillation cycle the system is in at the moment of the interaction. The light field then again drives the system in a periodic manner starting from this new state. Then the next interaction puts the system again into the ground or excited state, the oscillation starts again and so on.

As these interruptions of the evolution are probabilistic, after some time you cannot exactly predict anymore, in which state the system will be at a certain instant because you do not know anymore when the last interaction has happened and into which state the system was placed by the interaction. So to describe the system, you need to add up the different possible evolutions taking into account all interactions that may have happened weighted by the probability amplitude that they actually took place. For times that are significantly longer than the mean time between two interactions this smears out the oscillations.

 

[JD23]

Thank you, if I properly understood, the stimulated emission/absorption (also spontaneous emission) equations e.g. in https://en.wikipedia.org/wiki/Stimulated_emission#Mathematical_model are only effective approximations for large atomic populations - which break when loosing coherence of Rabi oscillations of individual atoms?

So shooting a proper frequency laser into two-level system target as population of atoms, we will first increase n2, but then n2 will start oscillating, reaching what level?
Naively we would say it should reach n2 for which the absorption and spontaneous emission equations equalize - but it neglects Rabi oscillations.
How would it change for real physics - including Rabi?

 

[Cthugha]

Thank you, if I properly understood, the stimulated emission/absorption (also spontaneous emission) equations e.g. in https://en.wikipedia.org/wiki/Stimulated_emission#Mathematical_model are only effective approximations for large atomic populations - which break when loosing coherence of Rabi oscillations of individual atoms?

They work reasonably well as soon as coherence is lost, but not while the coherence is fully there.
Whenever any of the atoms undergoes an interaction, it will be put in either the ground or the excited state and the Rabi oscillation will start again from this state. When there are many atoms and enough interactions have happened, so that any memory of the initial state is effectively lost, a stochastic treatment is fine and will in the end lead to the usual emission and absorption ratios.

So shooting a proper frequency laser into two-level system target as population of atoms, we will first increase n2, but then n2 will start oscillating, reaching what level?
Naively we would say it should reach n2 for which the absorption and spontaneous emission equations equalize - but it neglects Rabi oscillations.
How would it change for real physics - including Rabi?

If the mean time between two interaction events is long compared to the duration of a Rabi cycle, you will find that absorption and stimulated emission equalize. If the interactions are more frequent, then things start to change. Rabi oscillations drive the probability amplitude to find the system in a sinusoidal manner and the probability itself changes as the squared modulus of the probability amplitude. So the changes are pretty small close to the points, where the atoms are in the ground or excited state with 100% probability. The changes are strongly sublinear. If you interrupt the system so frequently that it never leaves the sublinear range, you will put it back into its initial state so frequently that you effectively "force" the state to never change, which is a very rough version of the quantum Zeno effect.