Optics: Image formed from a glass block

[Jahnavi]

Homework Statement

Homework Equations

The Attempt at a Solution

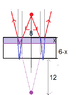
I have solved this problem . For that I had to use refraction at the first surface , then reflection from the back side and then again refraction from the first surface . This gives me the correct answer .

But when I saw the solution given I was quite surprised by the method employed . Please see the solution .

In this they consider the apparent position of the mirror (as if the mirror has shifted towards the object) .This is something similar when we look at the bottom surface of the pool and it appears nearer .

Even though this method gives the correct answer and is shorter, I wonder whether it is correct to employ this approach .

My objection is that the light rays have to actually travel all the way to the mirror so as to undergo reflection . In the pool case , it is the apparent shift which the observer standing from outside sees .

I would appreciate if someone could help me understand the validity of the above given solution .

 

[Orodruin]

The silvered surface is a bit of a red herring. It just mirrors everything so you could just as well ask for the image of an object held behind a 12 cm glass plate (with appropriate geometry for ”translating” the distances).

 

[Jahnavi]

Could you please explain a bit more .

 

[Orodruin]

It is difficult unless you can help in identifying which part of the computation you have a problem with.

 

[Jahnavi]

I don't have any problem in the computation . I would like to understand validity of this approach . Why we could consider as if the mirror has shifted towards the object ?

Consider the example of looking at the bottom of a pool . The rays originating from the bottom of the pool refract and on entering the observer's eye give the impression that the rays are coming from a nearer object (bottom of the pool) . It is how the bottom of the pool appears to the observer .

But in the given solution , it is considering as if the mirror has actually shifted towards the object . The shifting of the mirror doesn't look analogous to the case when an observer is perceiving the depth of an object (pool) .

How are the two cases analogous ?

It is the apparent shifting of the mirror which I fail to understand .

 

[Orodruin]

Consider the example of looking at the bottom of a pool . The rays originating from the bottom of the pool refract and on entering the observer's eye give the impression that the rays are coming from a nearer object (bottom of the pool) . It is how the bottom of the pool appears to the observer .

Why would it be any different in the mirror case? I don’t follow your logic in accepting one and not the other.

It is the actual shifting of the mirror which I fail to understand .

Obviously the mirror has not moved physically. But to get the correct image position you need to consider it moves. The question is where the image of an object on the mirror would be.

Again, the mirror you can remove by just mirroring the entire problem. You are then left with finding the shift of the image of an object held behind a 12 cm glass plate.

 

[Jahnavi]

But to get the correct image position you need to consider it moves.

Why ?

Why would it be any different in the mirror case?

Because it is not a case of how an observer (in air ) looking into the block perceives the depth of the mirror .

The rays originating from the object have to actually travel all through the width of the block so as to undergo reflection . It is not a matter of how things "look" from outside .

an object held behind a 12 cm glass plate.

I hope you mean " an object held 12 cm behind the glass plate " ?

 

[Orodruin]

Because it is not a case of how an observer (in air ) looking into the block perceives the depth of the mirror .

Why wouldn't it be? It is exactly like that, times two.

I hope you mean " an object held 12 cm behind the glass plate " ?

No. 6x2 = 12.

 

[Drakkith]

But in the given solution , it is considering as if the mirror has actually shifted towards the object . The shifting of the mirror doesn't look analogous to the case when an observer is perceiving the depth of an object (pool) .

Replace the mirror with something else. Perhaps a scratch. Does it make sense that the scratch appears 5 cm away instead of 6 cm?

 

[Charles Link]

@Jahnavi Because of the mirror, the problem is equivalent to a glass block that is 12 cm thick that has the object 8 cm behind the glass block=20 cm behind the front face. The image appears 12 cm behind the silvered face which is 18 cm behind the front face. (Once you see this part, you can then proceed to solve it, with a couple of the steps shown below). $\\$ There is perhaps a more standard way of computing this, but a simple ray trace of a ray at angle $\theta$ w.r.t. the horizontal coming from the source (from a point on the x-axis) 20 cm behind the front face will suffice. When that ray encounters the glass surface, by Snell's law for small angles, it will then have angle $\theta_1=\frac{\theta}{n}$ w.rt. the horizontal when it travels through the glass. It will then exit the front face, and once again, (by Snell's law), have angle $\theta$. This final ray can be traced back, and where it crosses the x-axis will be the location of the image. $\\$ You can write the vertical distance $y$ this ray traveled in air and in the glass block: $y=8 \tan(\theta)+12 \tan(\theta/n) =8 \, \theta+12 \, \theta /n$ for small angles. It is then easy to compute the distance $s_1$ from the front face that the final emerging ray, when traced backwards, will cross the x-axis: We just computed $y$. The emerging ray is traveling at angle $\theta$. Using $\tan(\theta) \approx \theta$ simplifies the calculation. Thereby the distance $s_1$ is such that $\theta=\frac{y}{s_1}$ ==>> $s_1=\frac{y}{\theta}$. $\\$ As a homework helper, I'm not supposed to give the complete solution, but see if you can follow the calculations I presented, and then compute the last couple of steps. $\\$ Additional item: Do you see that the final result for the distance $s_1$ that was computed is independent of the angle $\theta$ that was chosen? And they tell you what $s_1$ is. All you need to do is solve for $n$. $\\$ Edit: And I just saw the part in the OP where you have already solved this... I also am unable to follow the method that they are using in the posted solution of the OP.$\\$ Edit: Upon further study, I think I can almost see what they are doing, but they are using formulas for a case that really is not encountered very often. Normally images in optics come mostly from thin lenses and spherical reflective optics where paraxial rays are considered and the lensmakers formula applies. Only on rare occasion have I needed to do the case of an image from a thick block of glass or other transparent medium such as water. When I have, I simply derived the result, rather than trying to employ a formula.

 

[Jahnavi]

Hello Charles ,

Thank you for showing interest in this thread

I understand what is being done in the solution , but I don't understand why this approach is correct .

Now as to why I am interested in this solution is because this approach gets the answer very quickly ( we can even find the answer mentally ) and accurately .

The more systematic method (two refraction and one reflection ) is far more time consuming and we have to be a bit careful so as to avoid any error due to sign convention .

Even all the books are employing this quick approach .

This is why I am intrigued by this method .

Now as to what my objection is towards this method , I have already written in my replies above .

 

[Charles Link]

Hello Charles ,

Thank you for showing interest in this thread

I understand what is being done in the solution , but I don't understand why this approach is correct .

Now as to why I am interested in this solution is because this approach gets the answer very quickly ( we can even find the answer mentally ) and accurately .

The more systematic method (two refraction and one reflection ) is far more time consuming and we have to be a bit careful so as to avoid any error due to sign convention .

Even all the books are employing this quick approach .

This is why I am intrigued by this method .

Now as to what my objection is in this method , I have already written in my replies above .

How about the method that I used? It is very simple. $\\$ I am having difficulty following exactly what they are doing with what you are saying is a shorter way. It doesn't seem to be logical enough that I would ever incorporate the method.

 

[Jahnavi]

What happens when we look at the bottom of the pool from outside ? It looks as if the bottom is raised . There is an apparent shift .

In the OP they are employing the same approach , considering the apparent shift of the mirror . Why this approach gives correct result is puzzling me .

 

[Charles Link]

What happens when we look at the bottom of the pool from outside ? It looks as if the bottom is raised . There is an apparent shift .

In the OP they are employing the same approach , considering the apparent shift of the mirror . Why this approach gives correct result is puzzling me .

What they are doing I think is saying there is some plane that appears a distance $x$ below the surface from which we can then symmetrically map the image and object space. If we were to spend a couple hours dissecting it, we might be able to completely justify the method. There are some people who are very good at picking out hidden symmetries. This one isn't obvious to me.

 

[Charles Link]

One thing that seems to be missing here, in order to reach any good conclusions about this is a well-developed methodology of what the image looks like=i.e. how the apparent distance is affected when viewed through a block of glass. If the glass is thickness $D$, and we view something a distance $L_1$ behind the glass, how far away does it appear? If we now move that object to a distance $L_2$ behind the glass, does it appear to move a distance $L_2 -L_1$? Until we have established a couple of simple cases like this by analyzing them by the long ray trace method, employing any techniques like the one that is posted in the solution above is really rests on loose footing. $\\$ In looking over the equations (that I put together in my solution), it appears a material of index $n$ shortens the apparent distances in that material by a factor of $n$. Otherwise, if $n=1$, distances such as $L_2-L_1$ will remain $L_2-L_1$, even when viewed through a glass block of index $n$. With this information, it is starting to look like the method of solution in the OP may be a reasonable approach. $\\$ Let's apply what we learned: The surface of the mirror appears to be a distance (knowing that $n=1.2$) $x=5$ cm below the surface. When viewed in the reflection, the front surface will appear to be 5 cm behind the mirror and an object 8 cm above (in front of) the front surface will appear to be 13 cm behind where the mirror appears to be. (That's 18 cm behind the front face and 12 cm behind the silvered face). It's starting to get kind of simple, but it wasn't without first presenting the fundamentals...It looks like the solution in the OP is a valid solution.

 

[ehild]

AS @Drakkith suggested assume a scratch at the far side of the glass plate. It appears closer as the thickness of the plate. This is easy to prove. The light rays behave as if they came from that plane at shorter distance and there was no glass, but only air. And they would behave the same way when that face of the plate was silvered. Then you have a mirror, at distance x<6 cm from the front side of the plate - in air.
See picture. The red and blue lines are the real rays, but the red reflected rays are the same as if they had been reflected at the lilac line, the apparent mirror which is in air.
All the derivation is based on that apparent mirror in air, there is no glass any more.
That apparent mirror is at x distance form the front face of the plate. The object distance is x+8, the image distance is the same at he other side of the apparent mirror, x+8. But it was given that the image forms at 12 cm from the silvered face, so it is 6-x+12 from the apparent mirror, which has to be equal to 8+x. 8+x=6-x+12, x=5 cm.

 

[Jahnavi]

The light rays behave as if they came from that plane at shorter distance and there was no glass, but only air. And they would behave the same way when that face of the plate was silvered. Then you have a mirror, at distance x<6 cm from the front side of the plate - in air.
See picture. The red and blue lines are the real rays, but the red reflected rays are the same as if they had been reflected at the lilac line, the apparent mirror which is in air.
All the derivation is based on that apparent mirror in air, there is no glass any more.

Wonderful explanation !

Exactly what I wished to understand .

Thanks a lot .

 

[Jahnavi]

Thanks @Drakkith !

Thank you @Charles Link

 

[ehild]

Wonderful explanation !

Exactly what I wished to understand .

Thanks a lot .

I think, I have understood it at last