newbphysic
- 39
- 0
70.11 clockwiseehild said:The result are not same, only close together. What did you get with my method?
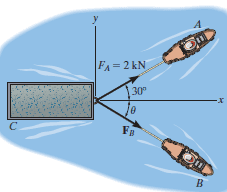
The discussion focuses on optimizing the forces in towing a truck using two ropes, specifically minimizing the force FB while maintaining a resultant force of 950 N directed along the positive x-axis. The angle of force FA is fixed at 20°. Participants derive equations for the x and y components of forces FA and FB, leading to the conclusion that the angle q for FB must be approximately 71.12° clockwise from the x-axis to achieve this minimum. The relationship between the angles FA and FB is established, confirming that they are complementary, thus reinforcing the geometric interpretation of the problem.
PREREQUISITESStudents in physics or engineering disciplines, particularly those focusing on mechanics, as well as professionals involved in optimizing towing systems and force applications.
70.11 clockwiseehild said:The result are not same, only close together. What did you get with my method?
ehild said:It should be 71.12 clockwise.
ehild said:There was some mistakes when we derived FB, and I did not notice.
Next time do the derivation symbolically, and plug in numerical data at the end. In that case, you would have got 70°.
It is true that the two angles add up to 90°.
If the angle of FA is a and the angle of FB is q, and the magnitude of the sum of the forces is F
FAcos(a) + FBcos(q) =F, (we measure q clockwise),
FA sin(a) = FB sin(q) --> FA=FB sin(q)/sin(a).
F_B=\frac{F}{\frac{\sin(q)}{\tan(a)}+\cos(q)}
If you want FB minumum, the denominator should be maximum. Take the derivative of ##\frac{\sin(q)}{\tan(a)}+\cos(q)## and make it equal to zero : ##\frac{\cos(q)}{\tan(a)}-\sin(q)=0##, that is ##\frac{1}{\tan(a)}-\tan(q)=0##
What does it mean for the angles a and q?
It's easy to see geometrically.newbphysic said:For FB perpendicular FA,is there an explanation for this ? why it works ?
It IS the explanation. ##\vec F_R ## is the sum of the vectors ##\vec F_A ## and ##\vec F_B ##. We expressed their components with the magnitudes FA, FB and angles, a, q. Solved the system of equations for FB. It must be minimum, so its derivative with respect to q has to be zero. From that, we got the equation ##\frac{1}{\tan(a)}-\tan(q)=0##, that is, the tangent of the angle q is equal the reciprocal of the tangent of the other angle. Now, remember how the tangent was defined in a right triangle,newbphysic said:For FB perpendicular FA,is there an explanation for this ? why it works ? and why not perpendicular to FR ?
Sorry if i ask a lot of questions :)
when it's perpendicular to FR ? the red line is the right answer according to calculationharuspex said:It's easy to see geometrically.
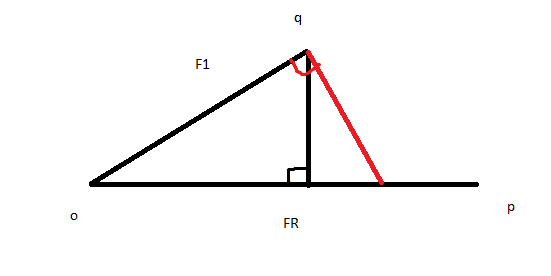
Draw the 950N as a line OP with a length representing its magnitude, and a line for the direction of FA from the same origin.
The magnitude of FA will be indicated by a point on its line, Q say.
FB will be represented by a vector from Q to P. What position of Q minimises the length PQ?

ehild said:##tan(\alpha)=a/b## and ##tan(\beta)=b/a##, the tangents of the two angles are reciprocal to each others in a right triangle. But the sum of the two angles is 90°as the sum of all angles in a triangle makes 180°, one angle is 90° , so ##\alpha + \beta = 90°##. Any time when the tangents of two acute angles are reciprocal, their sum is 90°.
Here, the two forces ##\vec F_A ## and ##\vec F_A ## enclose the angle a+q, and the tangents of the angles are reciprocal to each other, so a+q=90°, the forces are perpendicular to each other.
This is an other problem. Here Fa is given, FR has to be determined, so as its direction is the positive x axis. In the previous problem, FR was given and Fa was unknown.newbphysic said:OKbut what i still don't understand is this, how can you know it must be perpendicular to FA not to FR. Here is another example that looks exactly like before but in this example Fb perpendicular Fr. Why it's different ?

I tried to use the your method and i find theta = 60 degrees
I'm really confusedehild said:This is an other problem. Here Fa is given, FR has to be determined, so as its direction is the positive x axis. In the previous problem, FR was given and Fa was unknown.
From the equation Fa sin(30)=Fbsin(θ) ---> 2*1/2 = Fbsin(θ), you get that Fb=1/sin(θ), which is minimum if sin(θ)=1, that is, θ=90°.

Neither line minimises the distance PQ, keeping P fixed and varying Q. (Or is P supposed to be where the red line meets the baseline?)newbphysic said:when it's perpendicular to FR ? the red line is the right answer according to calculation
haruspex said:Neither line minimises the distance PQ, keeping P fixed and varying Q. (Or is P supposed to be where the red line meets the baseline?)
If one has a fixed direction and you are trying to minimise the other, yes.newbphysic said:P is fixed but Q vary.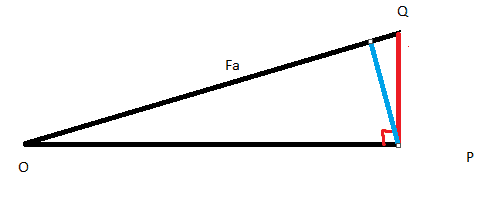
Ooh i see so is this mean in order to find minimum value the unknown must perpendicular to each other ?
In the first problem, FR was given, you knew the point P and you had to draw a line to the line of FA, which length was the shortest. It is the normal from P to the line FA. That line segment corresponded to FB, and the red line segment corresponded to FA.newbphysic said:I'm really confused
Why for the first problem i can't solve it like this one (without substituting FA)
FA sin(20) -FB sin(q) = 0
FB =FAsin(20)/sin(q)
I know that we don't know FA but we know in order for FB to be minimum sin(q) must equal 1 (the biggest value) but the result will not be 70
haruspex said:If one has a fixed direction and you are trying to minimise the other, yes.
(I assume Q in the diagram is where the blue line meets the sloping black line.)
Thank you for your helpehild said:In the first problem, FR was given, you knew the point P and you had to draw a line to the line of FA, which length was the shortest. It is the normal from P to the line FA. That line segment corresponded to FB, and the red line segment corresponded to FA.
In the second problem, FA was given, you knew the point Q. You have to draw the shortest line from it to the line of FR. It is perpendicular to FR.
You know, that the shortest distance from a point to a straight line is the perpendicular to the given line.
View attachment 97245
If you drew a line perpendicular from P, its length would be longer than the real FB.
View attachment 97246
