Optimizing Thrust and Operation Time for a CO2-Powered Rocket Torpedo Design

[Julez55]

TL;DR

I'm designing a torpedo that is propelled by compressed air, essentially it is a rocket. The challenging part is the torpedo needs to have a speed low enough such that getting hit by it will not leave a bruise. I need to determine what to pressurize the vessel to. The vessel will be a 12g CO2 cannister filled with compressed air.

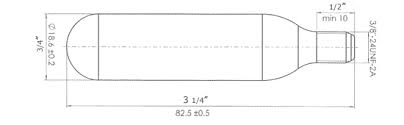
1. A CO2 canister with the following dimensions will be used.

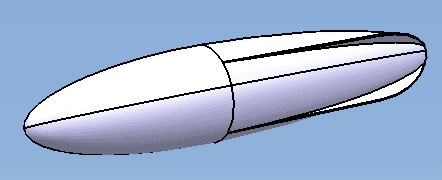
2. A shell was designed to house the CO2 canister, and the coefficient of drag was calculated to be 0.33

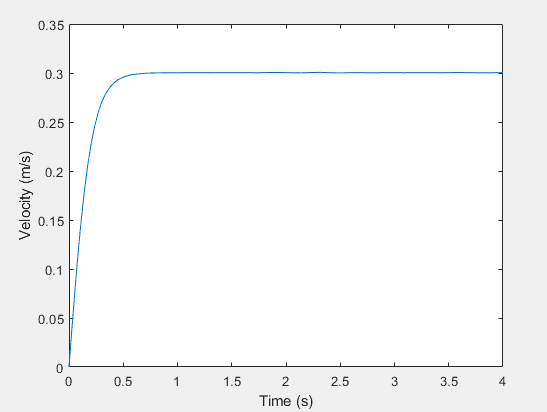
3. The constant thrust required to move the torpedo at approximately 1ft/s was found by using a free body diagram to generate an equation of motion for the torpedo: T(Po1) - D(ẋ) =mẍ, where D(ẋ) = =.5CdAẋ2. The ODE was solved in Matlab with variable thrust inputs. The thrust required to move the torpedo 1ft/s was determined to be a consntant .25N.

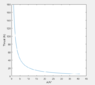
4. A Matlab code was generated to determine the Thrust as a function of A/A* using isentropic flow relations , where A* is the exit area of the CO2 cannister giving an exit velocity of M = 1.

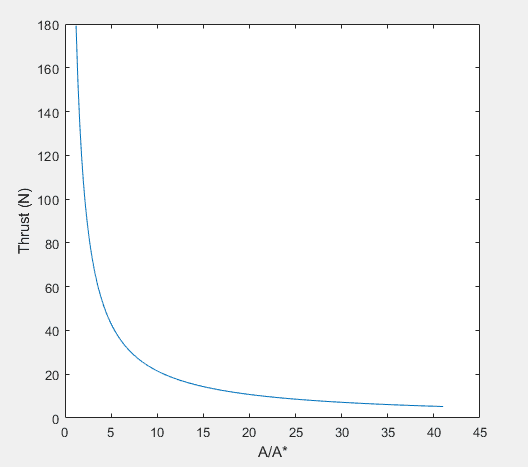
The figure of Trust versus the area ratio shows that thrust asymptotically approaches zero as the area ratio increases. For the configuration of the CO2 cannister A/A* = 4, and is therefore generating about 110 Newtons of thrust which is far too large.

My question is, is it possible with the given area ratio of the CO2 cannister to generate .25N of thrust? I feel like I hit a bit of a brick wall with my design, as I was planning to choke the flow.

A side question, as I had two professors tell me two different things. Let's say we have a choked flow with a constant A/A*, and P/P* = 2. One professor told me the Thrust will be constant as long as the Pressure ratio is above P/P*=2, yielding a constant massflow until the pressure ratio is below P/P*=2, this makes sense to me. The other professor told me if the pressure ratio is above P/P* = 2 the Thrust isn't constant and will have a mass flow as a function of time.

 

[phinds]

... essentially it is a rocket. The challenging part is the torpedo needs to have a speed low enough such that getting hit by it will not leave a bruise.

A "slow moving" rocket seems like a contradiction in terms.

 

[jrmichler]

When the pressure ratio is greater than about 2, the flow is choked. Search choked flow through orifice for some good resources. The flow rate in choked flow is proportional to the upstream density, which changes with pressure.

That small pressure vessel does not contain enough gas to push the rocket at constant speed. It will accelerate to a speed, then coast because it will be out of pressure. The correct way to analyze this is by numerical simulation. Start with a pressure, calculate flow, calculate thrust, calculate acceleration, calculate rate of pressure decrease, then start over at the next time step. Make the time steps small enough that the pressure changes less than 2% or 3% between steps. Keep in mind that the compressed gas temperature changes as the pressure drops. Then iterate the starting pressure until the rocket reaches your desired speed.

Then add in aerodynamic drag. I suspect that you will find that aerodynamic drag will have a negligible effect on the maximum speed, but you should find out for yourself.

 

[phinds]

It will accelerate to a speed, then coast because it will be out of pressure
...
Then add in aerodynamic drag. I suspect that you will find that aerodynamic drag will have a negligible effect on the maximum speed, but you should find out for yourself.

He's building a torpedo. You think maybe hydrodynamic drag will also be negligible?

 

[jrmichler]

OOPS, good catch. So hydrodynamic drag should be part of the simulation from the beginning.

 

[Julez55]

That small pressure vessel does not contain enough gas to push the rocket at constant speed. It will accelerate to a speed, then coast because it will be out of pressure.

I don't see how you can say that in absolute terms. My graph of velocity Vs time shows it would take the torpedo less than .5 seconds to accellerate to speed under .25N of thrust. If Po/Pe = 2 and the vessel was overpressurized to say 500psi surely the thrust would be constant for some time.

 

[Dullard]

You don't specify how long the torpedo needs to run, or what thrust (velocity) variation is acceptable. Those questions need answers before you can really make any useful design decisions.

 

[Dullard]

I'm going to assume that we have a language issue.

Does the torpedo need to operate for 1 second? 1 minute? 10 minutes?
Can the thrust vary +/- 1%? 10%? 100%?

For a simple pressure-fed orifice, the thrust will not be constant. How much decay occurs depends on how long you run the torpedo. You could 'over-fill' the tank if you can stand some initial 'excess thrust' - my second question.

There are other (less simple) ways to extend operation.