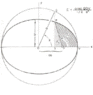
In an elliptical orbit, there are indeed two points where the instantaneous speed matches that of a circular orbit at the same radius, specifically at the perigee and apogee. The expressions for the speeds in circular and elliptical orbits are V = √(GM/R) for circular orbits and V = √(GM * (2/R - 1/a)) for elliptical orbits. The discussion highlights that while the speed is constant in circular orbits, it varies in elliptical orbits, being fastest at the lowest point and slowest at the highest. The key takeaway is that the intersection points of the two orbits indicate where the speeds are equal, and this can be represented graphically. Understanding these dynamics is crucial for analyzing orbital mechanics effectively.