Ziang
- 66
- 0
In the following link,
https://en.wikipedia.org/wiki/Geodesics_in_general_relativity
they write:"the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-D spacetime geometry around the star onto 3-D space."
Is there anything wrong with the following circular orbit of a missile around the Earth?
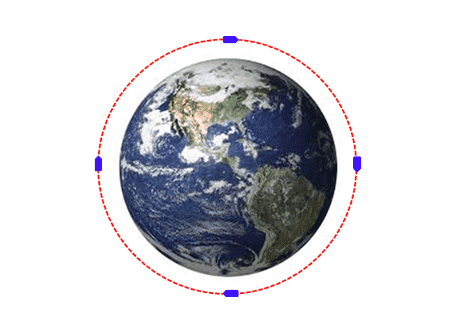
https://en.wikipedia.org/wiki/Geodesics_in_general_relativity
they write:"the path of a planet orbiting around a star is the projection of a geodesic of the curved 4-D spacetime geometry around the star onto 3-D space."
Is there anything wrong with the following circular orbit of a missile around the Earth?