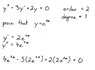- #1
Dr Game
- 26
- 0
I was taking notes in class and the prof said that in the equation
[tex]y^(double prime)-3y^(prime)+2y = 0[/tex] that 2 was the order.. is that due to the following?
the first y = 0 when you take the derivative twice
the second y = 0 when you derive it once
and the first one = 2 when you derive it once
Just a question.. shouldn't I derive the first one 3 time, and the second one 2 times, because you derive 2y once?
[tex]y^(double prime)-3y^(prime)+2y = 0[/tex] that 2 was the order.. is that due to the following?
the first y = 0 when you take the derivative twice
the second y = 0 when you derive it once
and the first one = 2 when you derive it once
Just a question.. shouldn't I derive the first one 3 time, and the second one 2 times, because you derive 2y once?