Orthogonality Relationship for Legendre Polynomials

[LCSphysicist]

Homework Statement

I am trying to orthogonalize {1,x,x²}

Relevant Equations

Just the inner product of functions space.

Suppose p = a + bx + cx².
I am trying to orthogonalize the basis {1,x,x²}
I finished finding {1,x,x²-(1/3)}, but this seems different from the second legendre polynomial.

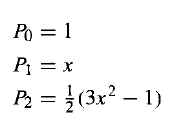
What is the problem here? I thought could be the a problem about orthonormalization, but check and is not.

 

[eys_physics]

Your basis is orthogonal but not orthonormal. You need to compute the normalization for your third basis function, i.e. $$\int_{-1}^1 dx (x^2 - 1/3)^2$$.

 

[LCSphysicist]

Your basis is orthogonal but not orthonormal. You need to compute the normalization for your third basis function, i.e. $$\int_{-1}^1 dx (x^2 - 1/3)^2$$.

Yeh, but as i said, i already do it. The integrate gives 8/45, taking the square and dividing by the module not get yet.

 

[LCSphysicist]

Vendo seu perfil, acho que daria pra te responder em portugues :D

 

[William Crawford]

Legendre polynomials are orthogonal but not orthonormal over the interval $[-1,1]$. Thus, you shouldn't expect your orthonormal basis to be identical to the Legendre polynomials.

NB. If you are trying to construct and orthonormal set $\{p_0,p_1,p_2\}$ of polynomials over the interval $[-1,1]$ from the set $\{1,x,x^2\}$ of monomials. Then the first two are $p_0(x) = \pm\frac{1}{\sqrt{2}}$ and $p_1(x) = \pm\sqrt{\frac{3}{2}}x$ and not $p_0(x) = 1$ and $p_1(x) = x$. As you can see, you have choice to make regarding the signs of $p_0(x)$ and $p_1(x)$.

 

[eys_physics]

The Legendre polynomials are usually normalized such that $P_n(1) = 1$.