Oscillation amplitude in oscillator

[Bromio]

Homework Statement

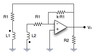
The circuit in attached figure behaves as an oscillator. What is the oscillation amplitude?

2. The attempt at a solution
With H(s), I've calculated the oscillation condition: KM \geq L_1+L_2, and the oscillation frequency: \omega = R_1/\sqrt(L_1 L_1 - M^2)

How can I obtain the amplitude of each oscillation?

Thank you.

 

[NascentOxygen]

The attached figure seems to have become detached.

 

[Bromio]

The attached figure seems to have become detached.

Thank you.

I've just attached the figure in this message.

 

[NascentOxygen]

In general, analysis of the linear circuit doesn't allow you to determine the amplitude of sinusoidal oscillations. The amplitude is determined by non-linearities which are built-in to the system, be they non-linearities in the amplifier, a soft diode clipper, or even just the rail voltage/s of the amplifier. Yes, this means that your sinewave oscillator doesn't generate a pure sinewave, there inevitably is going to be some distortion. (This doesn't mean it will necessarily be visibly distorted, though.)

 

[Bromio]

Thank you.

Certainly, the problem statement said: "Think about what could be the oscillation amplitude".

So, I suppose that, although I can't calculate the exact oscillation amplitude, I will be able to obtain an approximation. How can I do it? Maybe by Fourier series decomposition and taken the first harmonic?

Thank you, again.

 

[NascentOxygen]

In the absence of anything to limit the signal level, I don't think you can determine the amplitude. With a closed loop gain of 0.99999 you'll find that oscillation will not be maintained. Yet, the tiniest of increases to the gain, say, to 1.00001 then oscillations will build up without limit. You could simulate this with SPICE or some other package to see.

In the simulation you could then introduce gain-limiting parameters, such as the gain-bandwidth of the amplifier, or slew-rate limiting, or a diode limiter. In your circuit, you could introduce a tiny bit of B-H non-linearity (saturation in the transformer core) to see how that would limit the amplitude of oscillations.

 

[Bromio]

In the absence of anything to limit the signal level, I don't think you can determine the amplitude. With a closed loop gain of 0.99999 you'll find that oscillation will not be maintained. Yet, the tiniest of increases to the gain, say, to 1.00001 then oscillations will build up without limit. You could simulate this with SPICE or some other package to see.

In the simulation you could then introduce gain-limiting parameters, such as the gain-bandwidth of the amplifier, or slew-rate limiting, or a diode limiter. In your circuit, you could introduce a tiny bit of B-H non-linearity (saturation in the transformer core) to see how that would limit the amplitude of oscillations.

Thank you.

Because of this message, I've looking for something in the circuit to know how to estimate the amplitude. May the op-amp become saturation and so the amplitude is Vsat?

 

[NascentOxygen]

May the op-amp become saturation and so the amplitude is Vsat?

Certainly, the supply rails will always be a limiting factor on circuit operation.

 

[Bromio]

Certainly, the supply rails will always be a limiting factor on circuit operation.

OK.

Thank you.

 

[NascentOxygen]

It wouldn't be a good design though. Plug in a different amp with different o/p and the frequency would be different. Besides, the waveform would have to be horrible. (I'm assuming it's supposed to be a sinusoidal oscillator. The feedback resistors set a gain of less than unity over the entire bandwidth, but the inductor, with correct phasing, sidesteps this above some corner frequency.)

BTW, how did you explain the function of R2?