Oscillation of a mass connected to a spring displaced

[vishwesh]

Homework Statement

A mass m hangs on a spring of constant k. In the position of static equilibrium the length of the spring is l. If the mass is drawn sideways and then released,the ensuing motion will be a combination of (a) pendulum swings and (b) extension and compression of the spring. Without using a lot of mathematics, consider the behavior of this arrangement as a coupled system.

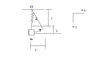
I have attached the figure I drew for this problem.

Homework Equations

The Attempt at a Solution

For x - direction:

$m \cfrac{d^2 x}{d t^2} + m {\omega_{0}}^2 x = 0$
$\implies \cfrac{d^2 x}{d t^2} + {\omega_{0}}^2 x = 0 \tag{1}$
$\implies \cfrac{d^2 x}{dt^2} + \cfrac{g}{l} x = 0\tag{1}$

For y - direction:

$m \cfrac {d^2 y}{d t^2} + ky = mg$
$\implies \cfrac{d^2 y}{d t^2} + \cfrac{k}{m} y = g \tag{2}$Solution for equation (1) would be:

$x = A \cos (\omega_{0} t) \tag{3}$

Solution for equation (2) would be:

$y = B \cos (\omega t) \tag{4}$

Am I on the right track and how should I proceed?

Thanks

 

[AlephNumbers]

Without using a lot of mathematics, consider the behavior of this arrangement as a coupled system.

I'm not sure what constitutes "a lot of mathematics". It sounds to me like the questioner just wants you to (maybe) mathematically express some of the initial conditions, and then offer a qualitative explanation of the overall behavior of the system.

I would advise you to wait to see someone else's take on the question, though.

 

[vishwesh]

I'm not sure what constitutes "a lot of mathematics". It sounds to me like the questioner just wants you to (maybe) mathematically express some of the initial conditions, and then offer a qualitative explanation of the overall behavior of the system.

I would advise you to wait to see someone else's take on the question, though.

Thanks for the reply. I will wait for some other responses.

 

[BvU]

Well, the problem statement in itself is already a bit strange to me: isn't there anything they want from you, other than that you 'consider' the system?

And your equations seem a bit strange to me. Do you mean to say that the spring doesn't exercise any force in the x-direction ?

 

[vishwesh]

Well, the problem statement in itself is already a bit strange to me: isn't there anything they want from you, other than that you 'consider' the system?

And your equations seem a bit strange to me. Do you mean to say that the spring doesn't exercise any force in the x-direction ?

Thanks for the reply. I am also stuck with what the question expects me to do. As for the force in x-direction, can you please tell me which other force will act ?

 

[BvU]

Wall, what if the spring is at ana ngle $\theta$ wrt the vertical when it has a length $l + \Delta l$ ?