Overall energy input in random vehicle vibration tests

[Roy1984]

Hello Everyone

I have got a question concerning the calculation of the overall energy input in random vehicle vibration tests.

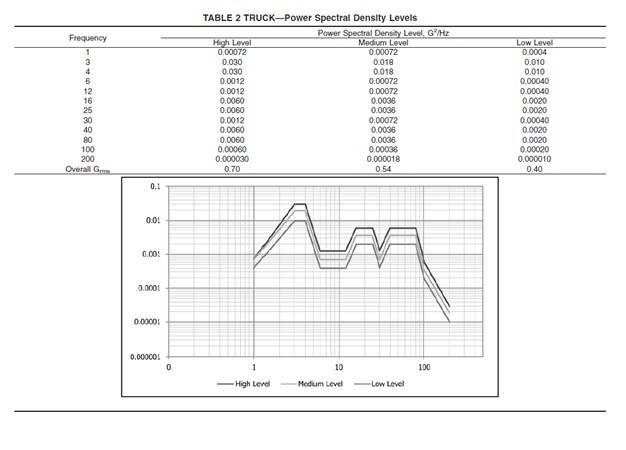
I have got different power spectral density levels for different random vehicle vibration tests and would like to compare them with each other concerning the overall energy input of the different tests. What I'm aware of is the following: The energy input definitely depends on the mass that is placed on a "shaker" for such a vibration test. Therefore I guess it would make sense to calculate an energy per mass for these different tests.

Besides the power spectral density levels, I already know the Grms value for the different levels. What I now would like to calculate is the energy-per-mass-input when such a test is performed for a certain time. So just comparing the Grms values doesn't do the trick, since I want to compare different tests with different running times and different power spectral density levels (and therefore different Grms values).

Here are some of the levels I would like to compare:

I hope anyone can help me on that subject. Thanks in advance.

Regards,
Roy

 

[Roy1984]

What I can add so far, or what I have tried before is the following (which didn't help me a lot):

Energy or work is defined as follows (units in [ ] ):
W = F*s = [N]*[m]

with:
[N] = [kg * m/s^2]

work follows:
W = [kg * m^2/s^2]

So work "W" per mass "m" is:
W/m = [m^2/s^2]

Now my problem is that I don't have a clue how I should calculate the input energy of such a power spectral density spectrum as shown above.

To my understanding the Grms value should be the relevant value. (https://en.wikipedia.org/wiki/Random_vibration: The root mean square acceleration (Grms) is the square root of the area under the ASD curve in the frequency domain. The Grms value is typically used to express the overall energy of a particular random vibration event and is a statistical value used in mechanical engineering for structural design and analysis purposes.)

But when I just multiply the Grms [m/s^2] value with the duration time of the test, the resulting unit is [m/s]. Which is not the unit [m^2/s^2] derived above for work per mass...

By the way: I don't necessarily need an exact value for the energy input per mass. What would be sufficient is a value I can claim to be proportional to the energy input, so I can compare different spectrums with each other.