Hello Panda Bear,
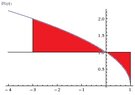
First, let's take a look at the region to be revolved:
View attachment 1100
Using the disk method, we see we will have two regions to revolve, the region on the left and the region on the right. However, since the radius is to be squared, and the radius on the right is the negative of the radius on the right, we may simply use one integral.
The volume of an arbitrary disk is:
$$dV=\pi r^2\,dx$$
where:
$$r=\pm\left(\sqrt{1-x}-1 \right)$$
and so we have:
$$dV=\pi\left(\sqrt{1-x}-1 \right)r^2\,dx=\pi\left(2-x-2\sqrt{1-x} \right)\,dx$$
Summing the disks by integrating, we have:
$$V=\pi\int_{-3}^1 2-x-2\sqrt{1-x}\,dx$$
For the third term in the integrand, let's use the substitution:
$$u=1-x\,\therefore\,du=-dx$$ and we have:
$$V=\pi\int_{-3}^1 2-x\,dx-2\pi\int_0^4u^{\frac{1}{2}}\,du$$
Applying the anti-derivative form of the FTOC, we find:
$$V=\pi\left(\left[2x-\frac{1}{2}x^2 \right]_{-3}^1-\frac{4}{3}\left[u^{\frac{3}{2}} \right]_0^4 \right)=$$
$$\pi\left(\left(\left(2(1)-\frac{1}{2}(1)^2 \right)-\left(2(-3)-\frac{1}{2}(-3)^2 \right) \right)-\frac{4}{3}\left(\left(4^{\frac{3}{2}} \right)-\left(0^{\frac{3}{2}} \right) \right) \right)=$$
$$\pi\left(12-\frac{32}{3} \right)=\frac{4\pi}{3}$$
We can check our work using the shell method. For the area on the left, we have:
The volume of an arbitrary shell is:
$$dV_1=2\pi rh\,dy$$
where:
$$r=y-1$$
$$h=\left(1-y^2 \right)-(-3)=4-y^2$$
and so we have:
$$dV_1=2\pi(y-1)\left(4-y^2 \right)\,dy=2\pi\left(-y^3+y^2+4y-4 \right)\,dy$$
Summing the shells, we find:
$$V_1=2\pi\int_1^2 -y^3+y^2+4y-4\,dy=2\pi\left[-\frac{1}{4}y^4+\frac{1}{3}y^3+2y^2-4y \right]_1^2=$$
$$2\pi\left(\left(-\frac{1}{4}(2)^4+\frac{1}{3}(2)^3+2(2)^2-4(2) \right)-\left(-\frac{1}{4}(1)^4+\frac{1}{3}(1)^3+2(1)^2-4(1) \right) \right)=$$
$$2\pi\left(\left(-4+\frac{8}{3}+8-8 \right)-\left(-\frac{1}{4}+\frac{1}{3}+2-4 \right) \right)=$$
$$2\pi\left(-\frac{4}{3}+\frac{23}{12} \right)=\frac{7\pi}{6}$$
Now, for the area on the right, we find the volume of an arbitrary shell is:
$$dV_2=2\pi rh\,dy$$
where:
$$r=1-y$$
$$h=1-\left(1-y^2 \right)=y^2$$
Hence:
$$dV_2=2\pi (1-y)\left(y^2 \right)\,dy=2\pi\left(y^2-y^3 \right)\,dy$$
Summing the shells, we find:
$$V_2=2\pi\int_0^1 y^2-y^3\,dy=2\pi\left[\frac{1}{3}y^3-\frac{1}{4}y^4 \right]_0^1=2\pi\left(\frac{1}{3}-\frac{1}{4} \right)=\frac{\pi}{6}$$
Adding the two volumes, we find the total is:
$$V=V_1+V_2=\frac{7\pi}{6}+\frac{\pi}{6}=\frac{4\pi}{3}$$