- #1
Bohrok
- 867
- 0
After recently studying Calc III on my own, I came across this problem with parametrizing the folium of Descartes.
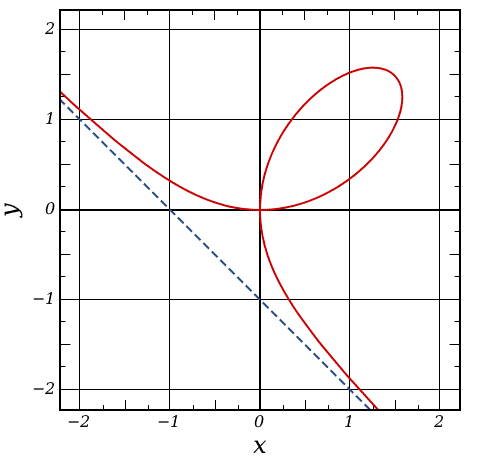
Show that for t ≠ -1, 0, the line y = tx intersects the folium at the origin and at one other point P. Express the coordinates of P in terms of t to obtain a parametrization of the folium.
The folium of Descartes is the curve with the equation x3 + y3 = 3axy, where a ≠ 0 is a constant.
I couldn't really get anywhere with this problem. I understand why t ≠ -1, 0, and y = tx → t = y/x.
Using the formula for the slope between two points with the origin (0, 0) and point P(x1, y1) on the folium went back to t = y/x
I know that x(t) = 3at/(t3 + 1) and y(t) = 3at2/(t3 + 1) from the Internet but I couldn't find a good explanation of the steps in deriving the parametric equations. They look quite similar to the previous problem in the book which would probably help with this problem, but I couldn't do anything useful with that problem either:
Show that the line of slope t through (-1, 0) intersects the unit circle in the point with coordinates x = (1-t2)/(t2 + 1), y = 2t/(t2 + 1)
Conclude that these equations parametrize the unit circle with the point (-1, 0) excluded. Show further that t = y/(x + 1)
Homework Statement
Show that for t ≠ -1, 0, the line y = tx intersects the folium at the origin and at one other point P. Express the coordinates of P in terms of t to obtain a parametrization of the folium.
Homework Equations
The folium of Descartes is the curve with the equation x3 + y3 = 3axy, where a ≠ 0 is a constant.
The Attempt at a Solution
I couldn't really get anywhere with this problem. I understand why t ≠ -1, 0, and y = tx → t = y/x.
Using the formula for the slope between two points with the origin (0, 0) and point P(x1, y1) on the folium went back to t = y/x
I know that x(t) = 3at/(t3 + 1) and y(t) = 3at2/(t3 + 1) from the Internet but I couldn't find a good explanation of the steps in deriving the parametric equations. They look quite similar to the previous problem in the book which would probably help with this problem, but I couldn't do anything useful with that problem either:
Show that the line of slope t through (-1, 0) intersects the unit circle in the point with coordinates x = (1-t2)/(t2 + 1), y = 2t/(t2 + 1)
Conclude that these equations parametrize the unit circle with the point (-1, 0) excluded. Show further that t = y/(x + 1)
