- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What Type of Signal is x(t) in Parseval's Theorem?
- Thread starter Jiho
- Start date
In summary, Parseval's theorem states that mathematically, x(t) can be any function that is either complex or real valued and has a continuous Fourier transform. This function can represent either voltage or power in a circuit. However, the usual interpretation of the theorem is in terms of energy, so if x(t) represents power, the theorem may not make sense in that context.
Physics news on Phys.org
- #2
Delta2
Gold Member
- 6,002
- 2,628
Mathematically, ##x(t)## can be any function ##x:\mathbb{R}\rightarrow\mathbb{C}## that is any complex valued function over the real line (or as a sub case any real valued function over the real line ##x:\mathbb{R}\rightarrow\mathbb{R}##) for which its continuous Fourier transform ##X(f)## exists . So it can be a function representing the (complex) voltage between two nodes of a circuit or the power between two nodes of a circuit.
However the usual interpretation of this theorem in signal analysis is that the two sides of the equation are just two different ways of computing the total energy of a signal ##x(t)## (a voltage or a current signal).
However the usual interpretation of this theorem in signal analysis is that the two sides of the equation are just two different ways of computing the total energy of a signal ##x(t)## (a voltage or a current signal).
- #3
Jiho
- 20
- 4
you mentioned it doesn't matter that signal x(t) represents voltage or power. But I can't understand if x(t) represent power,
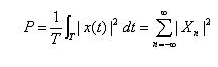 this equation doesn't make sense as I think. In my opinion, How can power^2 be just power?? Unit of dimension is not same as I know.
this equation doesn't make sense as I think. In my opinion, How can power^2 be just power?? Unit of dimension is not same as I know.
Attachments
- #4
Delta2
Gold Member
- 6,002
- 2,628
Yes I said that ##x(t)## can be any function for which the Fourier transform exists. However I also said that the usual interpretation is that of energy (the integrals in both sides represent energy) in the case ##x(t)## is a voltage or current signal. If ##x(t)## is a power signal then we can't give that usual interpretation of energy to this theorem.
FAQ: What Type of Signal is x(t) in Parseval's Theorem?
1. What is Parseval's Theorem?
Parseval's Theorem is a mathematical theorem that relates the energy of a signal in the time domain to the energy of its Fourier transform in the frequency domain. It states that the total energy of a signal can be calculated by integrating the squared magnitude of its Fourier transform.
2. What is the type of x(t) in Parseval's Theorem?
x(t) can be any continuous function in the time domain, as long as it satisfies certain conditions such as being absolutely integrable. This means that it must have a finite total energy and cannot have any infinite or undefined values.
3. How is Parseval's Theorem used in signal processing?
Parseval's Theorem is used to analyze signals in both the time and frequency domains. It allows for the calculation of the energy of a signal without having to compute its entire Fourier transform. This is useful in applications such as filtering, noise reduction, and spectral analysis.
4. Is Parseval's Theorem applicable to all types of signals?
Yes, Parseval's Theorem is applicable to all types of signals as long as they meet the necessary conditions. This includes both continuous and discrete signals, as well as periodic and non-periodic signals.
5. What are the limitations of Parseval's Theorem?
One limitation of Parseval's Theorem is that it only applies to signals with finite energy. This means that it cannot be used for signals with infinite energy, such as impulse signals. Additionally, it assumes that the signal is time-invariant, which may not always be the case in real-world applications.
Similar threads
- Replies
- 8
- Views
- 3K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Replies
- 9
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 1
- Views
- 790
- Replies
- 5
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 10
- Views
- 928
- Replies
- 1
- Views
- 1K
Share: