Partially rotated coordinate systems

Click For Summary
SUMMARY

The discussion centers on the mathematical derivation of partially rotated coordinate systems, specifically the transformation equations x' = x cos(θ) + y sin(θ) and y' = y cos(θ) - x sin(θ). These equations are crucial for understanding the rotation of axes in the context of special relativity. The user seeks clarity on these transformations to aid in deriving relevant formulas. A reference to a proof is provided from a calculus resource for further study.

PREREQUISITES
  • Understanding of trigonometric functions and their properties
  • Familiarity with coordinate systems and transformations
  • Basic knowledge of special relativity concepts
  • Ability to interpret mathematical proofs
NEXT STEPS
  • Study the derivation of rotation matrices in linear algebra
  • Explore the implications of coordinate transformations in special relativity
  • Learn about the geometric interpretation of trigonometric identities
  • Review the application of rotation of axes in physics problems
USEFUL FOR

Students of physics and mathematics, particularly those focusing on special relativity and coordinate transformations, will benefit from this discussion.

Bassalisk
Messages
946
Reaction score
2
Hello,

I am trying to understand this partially rotated coordinate systems.

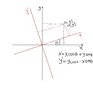
I do not understand how does x'=xcos(theta)+ysin(theta) and y'=ycos(theta)-xsin(theta)

I am probably stuck at silly answer but i need this to understand deriving of formulas for special relativity.

Thanks
 

Attachments

  • Untitled-2.jpg
    Untitled-2.jpg
    11.3 KB · Views: 2,085
Mathematics news on Phys.org

Similar threads

High School To calculate the polar unit vectors using rotated coordinates
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Transformations for isotropy in terms of math
  • · Replies 1 ·
Replies
1
Views
1K
High School How to find the infinitesimal coordinate transform along a hyperbola?
  • · Replies 1 ·
Replies
1
Views
1K
High School Invariant under rotation: Banal, obvious, or noteworthy?
  • · Replies 2 ·
Replies
2
Views
2K
Graduate How do I express an equation in Polar coordinates as a Cartesian one.
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Do we consider a point in a coordinate system to be a scalar?
  • · Replies 2 ·
Replies
2
Views
2K
High School Calculating the perfect tennis shot using vectors
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Area Differential in Cartesian and Polar Coordinates
  • · Replies 13 ·
Replies
13
Views
3K
Undergrad Plotting polar equations and scale invariance
  • · Replies 7 ·
Replies
7
Views
2K
High School Reprise: Calculate the distance between two points without using a coordinate system
  • · Replies 1 ·
Replies
1
Views
2K