aligator11
- 10
- 0
Thread moved from the technical forums, so no Template is shown
Summary: Mechanics problem related with Calculus (differential equations)
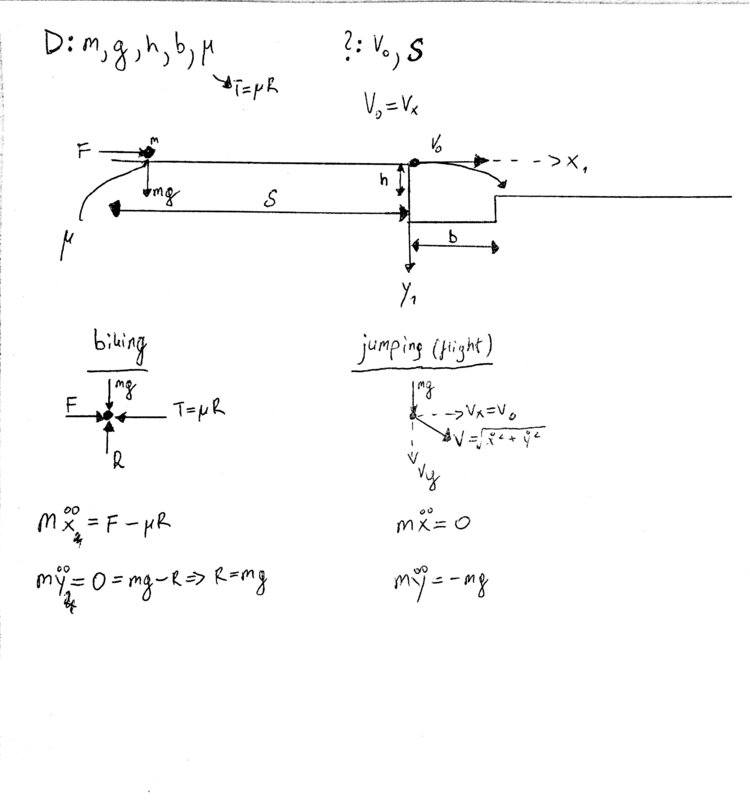
Hi everyone, I would like some help in that task, if anyone would be willing to help :) Namely I have a problem from particle dynamics. "D:" means given info... so, D: m,g,h,b, miu. We're looking for v0 and S as given on the diagram. We need to work out differential equation problems for that task and need to have initial conditions clearly stated.
Underneath the diagram you can see the forces I have already assigned onto the particle body diagrams.
Thanks for all the help I can get from you guys! :)
Hi everyone, I would like some help in that task, if anyone would be willing to help :) Namely I have a problem from particle dynamics. "D:" means given info... so, D: m,g,h,b, miu. We're looking for v0 and S as given on the diagram. We need to work out differential equation problems for that task and need to have initial conditions clearly stated.
Underneath the diagram you can see the forces I have already assigned onto the particle body diagrams.
Thanks for all the help I can get from you guys! :)