Homework Help Overview
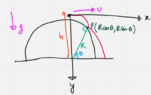
The discussion revolves around a particle projected from above a dome, following a parabolic trajectory. Participants explore the relationship between the particle's motion, its speed upon reaching the ground, and the geometry of the dome, particularly focusing on the angle of projection and the height at which the particle impacts the dome.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss the derivation of the final speed of the particle and its independence from the angle of projection, raising questions about the implications of energy conservation. There are attempts to clarify the conditions under which the particle collides with the dome and the assumptions regarding its trajectory. Some participants suggest that the problem may require the particle to touch the dome tangentially, leading to discussions about the necessary constraints on height and speed.
Discussion Status
The discussion is ongoing, with various interpretations of the problem being explored. Some participants have provided insights into the relationships between variables, while others express uncertainty about the clarity of the problem statement. There is a recognition that the calculations involved may be complex and that alternative approaches might be necessary.
Contextual Notes
Participants note potential ambiguities in the problem's wording, particularly regarding the conditions for the particle's interaction with the dome. There is also mention of the need for constraints to ensure that the particle impacts the dome at a tangent, which has not been definitively established in the discussion.