- #1
ChessEnthusiast
- 115
- 3
Let's say that we have two guys, each weighs 50 kg. They are pulling a piece of against each other as hard as they can. The tension of the rope will therefore be the force of friction acting on each of them (the same magnitude).
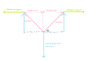
Now, let's say that a third person joins the party and grabs the rope right between them and wants to pull it in direction perpendicular to the rope.
Now, let's say that a third person joins the party and grabs the rope right between them and wants to pull it in direction perpendicular to the rope.
- What information do I need to estimate how much force is required to move the point where the third person holds the rope a certain distance in that direction?
- How does the tension of the rope after the pull depend on the initial tension, if the point moved the same distance in the perpendicular direction? For example, what difference would it make if the boys were 100 kg each instead?