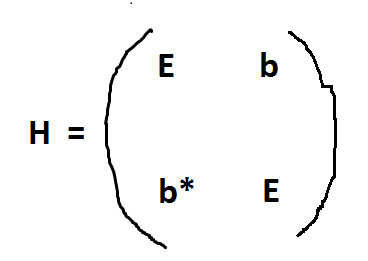SUMMARY
This discussion centers on the calculation of the first-order correction in Perturbation Theory (PT) within quantum mechanics. Participants reference key texts such as Sakurai, Gasiorowicz, Zettili, and Griffiths, highlighting that while first-order corrections are commonly covered, second-order corrections are also addressed in Griffiths' work. The conversation emphasizes the need for clear examples and methodologies for calculating these corrections, particularly for those struggling with higher-level texts.
PREREQUISITES
- Understanding of quantum mechanics principles
- Familiarity with Perturbation Theory concepts
- Knowledge of first-order and second-order corrections
- Ability to interpret mathematical formulations in quantum mechanics
NEXT STEPS
- Study the first-order correction methods in quantum mechanics using Sakurai's "Modern Quantum Mechanics"
- Explore second-order Perturbation Theory examples in Griffiths' "Introduction to Quantum Mechanics"
- Review Gasiorowicz's "Quantum Physics" for additional insights on PT
- Practice calculating first-order corrections with specific quantum systems
USEFUL FOR
Students and researchers in quantum mechanics, particularly those seeking to deepen their understanding of Perturbation Theory and its applications in solving quantum systems.