Phase Transitions in the Van Der Waals Gas

[GravityX]

Homework Statement

What does a minimum free energy mean for isothermal compressibility?

Relevant Equations

$\kappa_T=-\frac{1}{V}\Bigl( \frac{\partial V}{\partial P} \Bigr)_T=\frac{1}{V}\Bigl( \frac{\partial^2 F}{\partial V^2} \Bigr)^{-1}_T$

Hi,

I am not quite sure if I have understood the second task correctly, but I proceeded as follows.

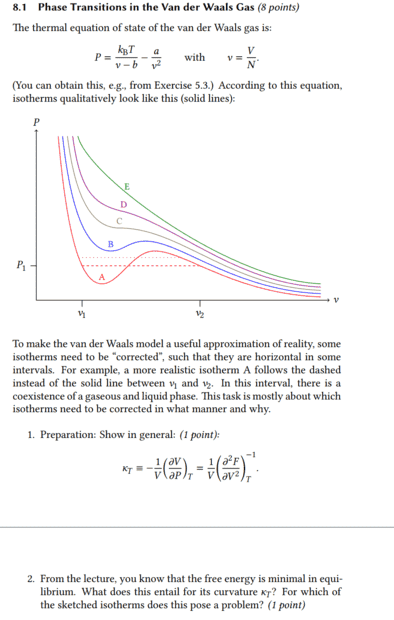
It's about what happens to the isothermal compressibility when the free energy becomes minimal. In the first task there was already the equation $\kappa_T=\frac{1}{V}\Bigl( \frac{\partial^2 F}{\partial V^2} \Bigr)^{-1}_T$ and I assume that this was not given without reason, but that one can use it to solve the second task.

If the free energy becomes minimal, then surely it means that the difference with $F_2$ < $F_1$ is therefore $F_2-F_1$ negative and thus also its derivative. Then the isothermal compressibility would be negative and thus left-curved.

 

[Chestermiller]

If the free energy is minimal for an isotherm, it means that the 2nd derivative of F with respect to V is positive.

 

[GravityX]

Thanks Chestermiller for your help

That would then mean that $\kappa_T$ would be curved to the left. If I have understood correctly, then $\kappa_T$ must always be positive for the system to be stable.

The problem says "For which of
the sketched isotherms does this pose a problem?" I would say for all but E, as this is continuously left curved.