GravityX
- 19
- 1
- Homework Statement
- What does a minimum free energy mean for isothermal compressibility?
- Relevant Equations
- ##\kappa_T=-\frac{1}{V}\Bigl( \frac{\partial V}{\partial P} \Bigr)_T=\frac{1}{V}\Bigl( \frac{\partial^2 F}{\partial V^2} \Bigr)^{-1}_T##
Hi,
I am not quite sure if I have understood the second task correctly, but I proceeded as follows.
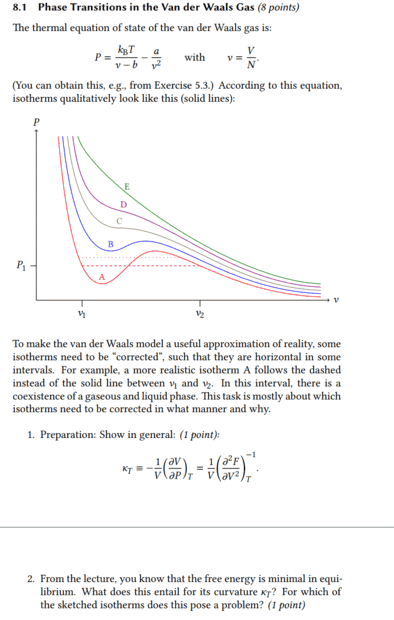
It's about what happens to the isothermal compressibility when the free energy becomes minimal. In the first task there was already the equation ##\kappa_T=\frac{1}{V}\Bigl( \frac{\partial^2 F}{\partial V^2} \Bigr)^{-1}_T## and I assume that this was not given without reason, but that one can use it to solve the second task.
If the free energy becomes minimal, then surely it means that the difference with ##F_2## < ##F_1## is therefore ##F_2-F_1## negative and thus also its derivative. Then the isothermal compressibility would be negative and thus left-curved.
I am not quite sure if I have understood the second task correctly, but I proceeded as follows.
It's about what happens to the isothermal compressibility when the free energy becomes minimal. In the first task there was already the equation ##\kappa_T=\frac{1}{V}\Bigl( \frac{\partial^2 F}{\partial V^2} \Bigr)^{-1}_T## and I assume that this was not given without reason, but that one can use it to solve the second task.
If the free energy becomes minimal, then surely it means that the difference with ##F_2## < ##F_1## is therefore ##F_2-F_1## negative and thus also its derivative. Then the isothermal compressibility would be negative and thus left-curved.