Physics - Elastic Collision: Solving for Unknowns

[J.live]

Homework Statement

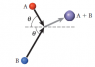
Two balls of equal mass collide and stick together as shown in the figure. The initial velocity of ball B is twice that of ball A. (Take θ = 56°.)

(a) Calculate the angle above the horizontal of the motion of mass A + B after the collision.

(b) What is the ratio of the final velocity of the mass A + B to the initial velocity of ball A, vf/vA?

(c) What is the ratio of the final energy of the system to the initial energy of the system, Ef/Ei?

The Attempt at a Solution

a) x= m ( 2vcos(56) + vcos(56) ) = 2mVfx

2vcos(56) + vcos(56)= mvfx

y = m ( 2vsin(56) + vsin(56) ) = 2mVfy

2vsin(56) + vsin(56) = 2mVfy

Am I suppose to take the magnitude of this ? How do I solve for two unknowns ?
Do all the m's and v's cancel out?

Thanks

 

[Quinzio]

y = m ( 2vsin(56) + vsin(56) ) = 2mVfy

2vsin(56) + vsin(56) = 2mVfy

There is something bad in the setup of the first equation.

Am I suppose to take the magnitude of this ? How do I solve for two unknowns ?
Do all the m's and v's cancel out?

Divide by the total mass of the body.
v remains.

 

[J.live]

2vcos(56) + vcos(56) = 2vfx => 3vcos(56)

2vsin(56) + -vsin(56) = 2vfy => vsin(56)

tan-1 ( y/x) => (1/3) => 26.3 degree