baby_1
- 159
- 16
Member warned about posting without the homework template
Hello
Here is my question
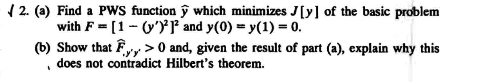
So I solved Euler DE and find
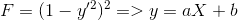
and when we apply the boundary condition we obtain y=0 . My teacher said that we should write it as two different function as
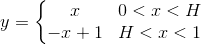
where H is (1/2).He solved this equation with this way
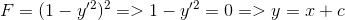
So Here are my questions:
a) why don't we accept the y=0 as our desire function?
b)how can obtain (a) constant in my equation with Euler approach?because in multidisciplinary function we can't find a ?
Here is my question
So I solved Euler DE and find
and when we apply the boundary condition we obtain y=0 . My teacher said that we should write it as two different function as
where H is (1/2).He solved this equation with this way
So Here are my questions:
a) why don't we accept the y=0 as our desire function?
b)how can obtain (a) constant in my equation with Euler approach?because in multidisciplinary function we can't find a ?