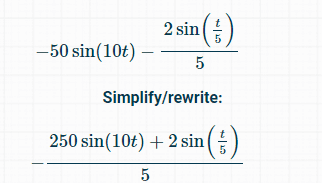Homework Help Overview
The discussion revolves around a physics problem involving the position function Z(t) of a plane flying across the Atlantic Ocean, focusing on the derivation of acceleration through differentiation and the interpretation of the variable 't'.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants explore the meaning of 't' in the context of acceleration, question the implications of taking derivatives, and discuss the conditions for maximum and minimum values of sine functions. There are attempts to analyze the relationship between the two sine functions involved and their respective maximums.
Discussion Status
The discussion is active, with participants offering insights into the mathematical properties of sine functions and their implications for the problem. Some participants suggest numerical methods due to the complexity of finding analytical solutions, while others provide guidance on the significance of the coefficients in the equations.
Contextual Notes
There are mentions of constraints regarding the use of radians versus degrees and the need for significant digits in the final answer. Participants also express uncertainty about the analytical approach and the physical interpretation of the mathematical results.