Ishika_96_sparkles
- 57
- 22
- TL;DR Summary
- I plotted a few curves for the wavefunction of Quantum Harmonic oscillator problem with certain energy values. The plotlegends do not seem to work in the final output.
Here, are the parts of the plot function[CODE title="plot I"]p1 = Plot[Normal[g*Exp[-x^2/2] /. solute[[1]] /. en -> 3], {x, -8, 8},
PlotStyle -> {Dashed, Gray}, PlotLegends -> Automatic];
(* Here, g=1 - x^2 - x^4/6 - x^6/30 - x^8/168 - x^10/1080 , energy en =3 and solute is the series solution of g with unknown coefficients*)[/CODE][CODE title="plot II"]p2 = Plot[
Normal[g*Exp[-x^2/2] /. solute[[1]] /. en -> 10], {x, -8, 8},
PlotStyle -> {Dashed, Red}, PlotLegends -> Automatic];
(* Here, g=1 - (9 x^2)/2 + (15 x^4)/8 - x^6/16 - (3 x^8)/896 - x^10/3840 *)[/CODE]
[CODE title="plot III"]p3 = Plot[
Normal[g*Exp[-x^2/2] /. solute[[1]] /. en -> 17], {x, -8, 8},
PlotStyle -> {Thick, Black}, PlotLegends -> Automatic];
(* Here, g= 1 - 8 x^2 + 8 x^4 - (32 x^6)/15 + (16 x^8)/105 *)
[/CODE]
and then the SHOW command as follows
[CODE title="Show command"]
Show[{p1, p2, p3}, PlotRange -> All,
LabelStyle -> Directive[Blue, Italic, 12]][/CODE]
What did I do wrong, here?
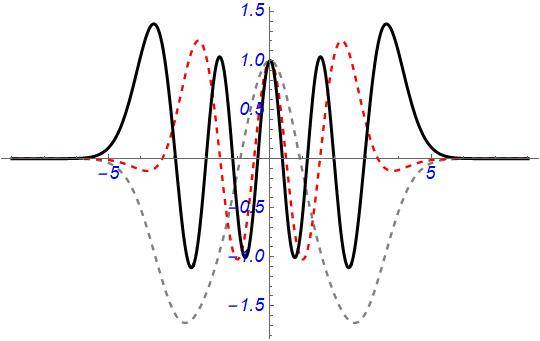
PlotStyle -> {Dashed, Gray}, PlotLegends -> Automatic];
(* Here, g=1 - x^2 - x^4/6 - x^6/30 - x^8/168 - x^10/1080 , energy en =3 and solute is the series solution of g with unknown coefficients*)[/CODE][CODE title="plot II"]p2 = Plot[
Normal[g*Exp[-x^2/2] /. solute[[1]] /. en -> 10], {x, -8, 8},
PlotStyle -> {Dashed, Red}, PlotLegends -> Automatic];
(* Here, g=1 - (9 x^2)/2 + (15 x^4)/8 - x^6/16 - (3 x^8)/896 - x^10/3840 *)[/CODE]
[CODE title="plot III"]p3 = Plot[
Normal[g*Exp[-x^2/2] /. solute[[1]] /. en -> 17], {x, -8, 8},
PlotStyle -> {Thick, Black}, PlotLegends -> Automatic];
(* Here, g= 1 - 8 x^2 + 8 x^4 - (32 x^6)/15 + (16 x^8)/105 *)
[/CODE]
and then the SHOW command as follows
[CODE title="Show command"]
Show[{p1, p2, p3}, PlotRange -> All,
LabelStyle -> Directive[Blue, Italic, 12]][/CODE]
What did I do wrong, here?