Plotting points in three-dimensional space

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

,
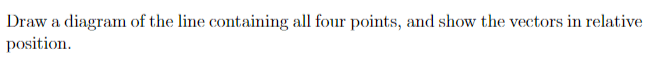The four points are,
$P(8,2,6)$
$R(-2,16,-2)$
$Q(3.9,2)$
$S(\frac{14}{3}, \frac{20}{3}, \frac{10}{3})$

And the solution is,

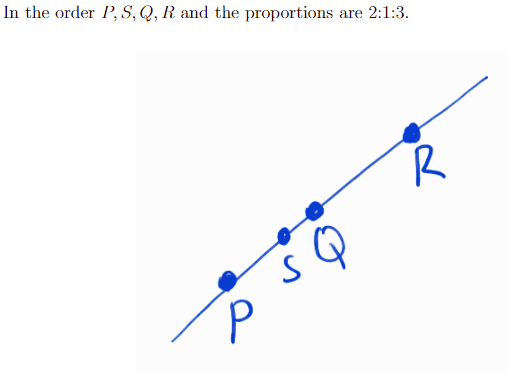
However, does someone please know what in the proportion 2:1:3 mean?

Many thanks!

 

[renormalize]

However, does someone please know what in the proportion 2:1:3 mean?

 

[ChiralSuperfields]

View attachment 325854

Thank you for your reply @renormalize !

I guess I can see where the comes from if we use a ruler to find the ratio.

However, how dose one know that without the drawing?

Many thanks!

 

[renormalize]

However, how dose one know that without the drawing?

You are given the $(x,y,z)$ coordinates of each of the 4 points $P,Q,R,S$. Can you can plot them in 3D space to see where they fall along the line? Do you know how to subtract two vectors to get their difference vector? And can you calculate the length of the difference vector to get the distance between the tips of those two vectors? (P.S.: "does" not "dose".)

 

[ChiralSuperfields]

You are given the $(x,y,z)$ coordinates of each of the 4 points $P,Q,R,S$. Can you can plot them in 3D space to see where they fall along the line? Do you know how to subtract two vectors to get their difference vector? And can you calculate the length of the difference vector to get the distance between the tips of those two vectors? (P.S.: "does" not "dose".)

Thank you for your reply @renormalize !

True it would be hard to tell which points are in which order if we did not graph the points in 3D space. Oh I now see. So if we find the magnitude of the difference vector between adjacent points then we should be able to find the ratio between them.

Many thanks!

 

[Steve4Physics]

True it would be hard to tell which points are in which order if we did not graph the points in 3D space. Oh I now see. So if we find the magnitude of the difference vector between adjacent points then we should be able to find the ratio between them.

To help get the ordering, you can also find the distances between pairs of non-adjacent points. For example, the pair of points with the biggest distance between them must be at the ends.

To simplify the arithmetic, a 'trick' you could use is to change all coordinate-scales by a factor of 3 to get rid of the thirds.
$S' = (3*\frac{14}{3}, 3*\frac{20}{3}, 3*\frac{10}{3}) = (14, 20, 10)$
$P' = (3*8,3*2,3*6) = (24, 6, 18)$
etc.

The order and relative spacing of $P', Q', R'$, and $S'$ are the same as those of $P, Q, R$ and $S$. But you don't have to work with the messy thirds. (But if you are not completely clear why that works, stick to using thirds.)

EDIT. A simpler way to get the order is to find how far each point is from the origin.
That won't always work, so struck-through.

 

[Mark44]

However, how dose one know that without the drawing?

 

[BvU]

I had fun plotting things -- and, being lazy, realized a 3D plot isn't necessary: 2D, e.g. the projection on the XY plane, is already enough:

$\$

 

[Steve4Physics]

I had fun plotting things -- and, being lazy, realized a 3D plot isn't necessary: 2D, e.g. the projection on the XY plane, is already enough

In fact 1D is enough! Only the x-coordinates are required to answer the question. (Or alternatively, only the y or only the z ones.)