B Poisson distribution having variation coefficient = .5?

[Addez123]

TL;DR Summary

How is it possible for a variation coefficient of poisson distribution to be anything other than 1?

Variation coefficient is calculated by

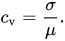
And the very definition of poisson distribution is that
$$\mu = \sigma $$

So how would any other value but 1 be a possible?

 

[gleem]

μ = σ²

 

[Addez123]

μ = σ²

Then its no longer a poisson distribution because the very definition of a poisson distribution is that
μ = σ, not μ = σ²

 

[gleem]

For a Poisson distribution, the mean is equal to the variance. Check your source.

 

[Addez123]

I see what I did wrong. I mixed up variance and standard deviation.