Position of the image of an object placed in water

[lorenz0]

Homework Statement

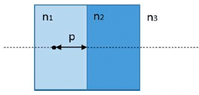
A glass plate of width $s = 3 cm$ with refraction index $n_2 = 1.5$ is in contact with water ($n_1 = 1.33$) on the left and with air on the right. An object is $p = 10 cm$ from the slab. Determine where the image of the object is formed.

Relevant Equations

$\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}$

I tried using the formula for the refraction of a spherical lens $\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}$ consider each slab as a spherical lens with curvature $R=\infty$ and by doing that I get $\frac{1.33}{10}+\frac{1.5}{q}=0\Leftrightarrow q\approx -11.3 cm$. Since the piece of glass has a width $s$ I suppose I should count $11.3 cm$ to the left of its rightmost edge, so the object should be $8.3 cm$ to the left of the leftmost edge of the piece of glass i.e. $1.7 cm$ to the right of the original object.

Does this make sense? I had never seen before a problem with "rectangular" lenses and three different materials, so I tried to adapt what I already know to this case. Thanks

 

[TSny]

I tried using the formula for the refraction of a spherical lens $\frac{n_1}{p}+\frac{n_2}{q}=\frac{n_2-n_1}{R}$

This is the formula for refraction at a spherical surface. The slab has two surfaces. So, you'll use the formula twice. The image of the first surface serves as the object for the second surface.

 

[lorenz0]

This is the formula for refraction at a spherical surface. The slab has two surfaces. So, you'll use the formula twice. The image of the first surface serves as the object for the second surface.

So, if I understand correctly, since from the first application of the equation I get that $q=-11.3 cm$ it means that the first image is formed $1.3 cm$ to the left of the original object, and applying it a second time I get $\frac{1.5}{11.3+3}+\frac{1}{q}=\frac{1-1.5}{\infty}\Leftrightarrow q\approx -9.53 cm$ so the second and final image appears $9.53 cm$ to the left of the rightward surface of the glass which implies, since the glass has a thickness of $3cm$, that it appears $3.47 cm$ to the right of the original image. Is this correct? Thanks

 

[rude man]

I think the problem statement needs clarification:
- object is in water or in air?
- object is 10 cm to the left or the right edge of the plate?

 

[lorenz0]

I think the problem statement needs clarification:
- object is in water or in air?
- object is 10 cm to the left or the right edge of the plate?

Looking at the image describing the problem, the object starts inside the water, $p=10cm$ to the left of the leftmost surface of the glass.

 

[TSny]

So, if I understand correctly, since from the first application of the equation I get that $q=-11.3 cm$ it means that the first image is formed $1.3 cm$ to the left of the original object, and applying it a second time I get $\frac{1.5}{11.3+3}+\frac{1}{q}=\frac{1-1.5}{\infty}\Leftrightarrow q\approx -9.53 cm$ so the second and final image appears $9.53 cm$ to the left of the rightward surface of the glass which implies, since the glass has a thickness of $3cm$, that it appears $3.47 cm$ to the right of the original image. Is this correct? Thanks

Your work looks good. It would be better to say that the final image appears $3.47$ cm to the right of the original object, rather than to the right of the original image.

 

[rude man]

Looking at the image describing the problem, the object starts inside the water, $p=10cm$ to the left of the leftmost surface of the glass.

Check. Thanks.

 

[rude man]

Using only Snell's law and small-angle approx. I can corroborate the answer. Do we agree it's a virtual image?

 

[lorenz0]

Using only Snell's law and small-angle approx. I can corroborate the answer. Do we agree it's a virtual image?

Yes, I do agree. Thank you.