D H said:
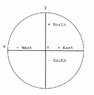
That's for converting polar coordinates to cartesian, AC130Nav. Latitude and longitude are not polar coordinates for one thing (the Earth is not spherical). Moreover, and much more importantly, there is no way to convert azimuth and elevation to either latitude and longitude or cartesian x/y/z. There are two reasons. First off, you need to know distance. Azimuth and elevation specify a direction, not a coordinate. Secondly, you need to know the latitude, longitude, and altitude of the observer. Think of it this way: The azimuth and elevation of the Moon are quite different for observers in New York and in California who see the Moon at the same time. Azimuth and elevation are local coordinates.
My apologies to all that the Wiki article didn't go far enough and I didn't look closely enough.
Actually, DH, it happens latitude and longitude are SPHERICAL Polar Coordinates, and it doesn't matter that the Earth isn't sperical (not that the k80sg specified that he was talking about the Earth, there's also the celestial spere), because the coordinates are essentially angles. (Did you know that the length of a nautical mile is variable?)
Navigation is not yet the subject of this thread, since K80sg hasn't specified; and I wouldn't
use the moon by preference for a navigation example because it's apparent motion is more
irregular. Let's say, however, you happen to know where the subpoint of the moon was at the time you measured its bearing and height; you would then know roughly where you are. The assumed position of the observed is used for plotting (because the great circle of equidistance from the subpoint is too large to plot and generally too far away for the bearing to make any sense) and knowing where approximately to look for a star among the myriads. I'm not sure this has anything to do with the question, though.
The distance from the center of the Earth (if there can be considered to be such a point) is
significant in calculating xyz coordinates in that it is the radius in the trig equations. It is
hard to determine to any degree of accuracy (although the GPS people are continually bettering their capability); however, we still don't know if that's what k80sg had in mind.
So playaone1 is quite right in so far as he went. Maybe some illustration will help with the
homework without giving all the math away: