Potential difference between two points in an electric field

[NoahCygnus]

Homework Statement

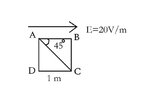
In the problem, I have to calculate the potential difference between C and A as in the uniform electric field of magnitude 20 V/m given in the figure.

Relevant Equations

$\Delta V = -\vec{E}\cdot\Delta\vec{r}$

So I have been given a uniform electric field $\vec{E}=20 V/m$ in the direction as show in the image. I have been told to calculate the potential difference $VC - VA$. According to the teacher (on YouTube) the potential difference $VC - VA = -10\sqrt{2}V$. But I say it's $-20 V$ as electric field is conservative and I can find potential difference as work done in moving a unit charge from $A$ to $D$ then to $C$. Potential difference between $D$and $A$ should be a big zero as we are moving perpendicular to the field and potential difference between $C$ and $D$ is $-20V$ so the overall potential difference between $C$ and $A$ should be $-20V$ and not $-10\sqrt{2}$.

They used $\Delta V = -\vec{E}\cdot\Delta\vec{r}$, and put in the values $\Delta V = -(20)(1)cos(45)=-10\sqrt{2}$

 

[Orodruin]

Their problem is that the length of the diagonal is not 1 m, it is $\sqrt 2$ m.

Edit: You should probably also link to the relevant video if it is on YouTube.