Potential Energy (A box attached to a spring which is attached to the ceiling.)

[LeonGrande]

Hello everyone!

To start things off, I apologize if this thread does not go here.

Today I had a test on Energy (Potential, Kinetic, Elastic) and we had a question which asked us to find out the value of k for a spring. The question was centered around a box hanging from a ceiling via a spring. Some velocity and other things were involved but I believe they will be irrelevant to what I want to know.

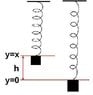
What I wish to know is, when an object is suspended above the ground, and it’s attached to the ceiling via a spring, why is it that you can use E_p=m*g*h to aid in solving the problem? The reason why this confuses me so much is that the height that is used to solve the question is given from x? But isn’t x the distance to the ceiling, not the distance to the ground? So why would this work? And since it does, why are you using the acceleration to gravity?

Relevant equations

E_e=E_k+E_p

(k*x²)/2=(m*v²)/2+m*g*h

x=h <----- this is where I am confused.

 

[6Stang7]

One thing you must remember about potential energy is that it's all relative. You can choose where you want your zero potential line to be. Depending on the specifics of the problem, it might have been easier to have the reference at the ceiling. That and the change in height from the box to the ceiling is the same as the box to the ground.

Can you not recall the specifics of the problem; your explanation is a little vague.

 

[LeonGrande]

I can. I just really wanted to know why it is that you can use E_p to solve a question like this.
I also asked my teacher this question after the test, and she told me as well it's all relative. But then I asked her why you can use gravity? Especially if the acceleration of gravity is in the opposite direction of the ceiling.
I think that's what really has me confused.

Here's the question as far as I can remember...

A box is attached to a spring which is attached to the ceiling. The mass of the box is 0.256kg. The spring is stretched 18.3cm, and then released. The resulting speed of the box is 0.754m/s when crossing the point of equilibrium. Find the force constant of the spring. I think... that is all that was in the problem, this is all from the top of my head.

 

[hikaru1221]

I'm not sure if I got what you meant. Maybe it's like this (see the picture). The left image is when the spring is unstretched, and the right one is when it is stretched 18.3cm. If I choose E_P=0 at y=0, then at y=x, E_P(x) = mgh = mgx. At y=0, total energy = E_e = 0.5kx², and at y=x, total energy = E_P + E_K = mgx + 0.5mv². Is this what you mean?

 

[6Stang7]

So, your teacher stated that:

Ee=Ek+Ep

(k*x2)/2=(m*v2)/2+m*g*h

where x=h



?

 

[LeonGrande]

The length in the stretch of the spring is represented by x. And x can also be used as h.

E_e=(k*x²)/2

E_p=m*g*h

After substituting all the values, k can be solved for.Edit: that is correct, 6stang7.

 

[6Stang7]

I think the issue here is what she means by "equilibrium position." When I think of a mass and spring system hanging from the ceiling, I consider the equilibrium to be the point where the net force is zero. However, she is considering the equilibrium point to be the location where the total energy in the spring is zero.

Using hikaru1221 diagram

it must be noted that at y=x, there is net force on the box is not zero. In this case, the equation she gave is correct.

 

[hikaru1221]

I guess the OP is stuck with choosing the origin of gravitational energy. Anyway I agree with 6Stang7; the term "equilibrium position" should be made clearer whether it is the equilibrium position of the system or that of the spring only.

Just one more thing to clarify what 6Stang7 said about solving (1/2)mv^2=(1/2)kx^2 for k. Here (in that equation ONLY) x is not 18.3cm; x is the displacement of the spring counting from the equilibrium position of the SYSTEM.

 

[6Stang7]

I deleted that section because I was worried that would confuse him, but yes, you are absolutely correct.

 

[LeonGrande]

I solved the question already during the test, and got it correct.
I just wanted to know the reasoning behind why E_p is still usable in a direction against gravity. I thought the whole reasoning behind E_p was that when an object is lifted from the ground upwards, it's potential energy is increased the higher it goes because of the pull of gravity. Now in this case of the box attached to the ceiling through the spring, I don't see how it's viable because E_p contains g.
I guess I worded what I wanted out of this post incorrectly.

 

[hikaru1221]

I just wanted to know the reasoning behind why E_p is still usable in a direction against gravity.

I'm not sure what you mean by direction of E_p. Do you mean that E_p is supposed to be smaller as going higher and vice versa?

 

[LeonGrande]

Ok, I made a diagram to bring some clarity to the confusing mumbo jumbo I have written :P

Like I stated earlier my confusion lies within the fact that you can use x as the height in the equation E_p. Why is this viable? I thought you needed the height of the object ABOVE the ground.

So why is it okay to use x, and still get an answer that makes sense? Just need clarification on the theory.

I hope this clears up what I am asking now -- if not I'll get my girlfriend to translate what I am asking into something comprehensible. Sorry I'm just one of those people who needs to know why, I can't help it. :-|

 

[hikaru1221]

Ah I see the problem now. It's completely wrong. But replacing x by h doesn't make it any better. Now assume that the equilibrium position referred in the problem is the position where the spring is at its natural length. I'll use your latest picture. Here is why:
_ At first, when the spring is stretched 18.3cm, there is elastic energy 0.5k\Delta x^2 and gravitational energy mgh_1 if you choose Ep=0 at h=0. Note that \Delta x = x - (natural-length-of-spring)=18.3cm.
_ Then there is kinetic energy and gravitational energy mgh_2.
_ We shall have: 0.5k\Delta x^2+mgh_1=0.5mv^2+mgh_2
Notice that h_2-h_1=\Delta x, we shall have:
0.5k\Delta x^2=0.5mv^2+mg\Delta x

You should note that \Delta x is not x.

 

[LeonGrande]

This makes a lot more sense to me.
Thank you, hikaru!