Potentiometer circuit for comparison of two resistances

[Prashasti]

Question :
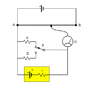
Figure shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X.

Isn't the question wrong?

I've searched for it everywhere, but didn't get the correct solution.
[URL="http://www.meritnation.com/cbse/class12-science/ncert-solutions/physics/physics-part-i---ncert-solution/current-electricity/page131-exercise-qno3.23/1368_247_6706/figure-334-shows-apotentiometer-circuit-for-comparison[/URL]

In the link, again, what they have done is,

iR/iX = l₁/l₂
So, R/X = l₁/l₂

How can the current passing through X be equal to that passing through R?

 

[gneill]

Your link doesn't take me to a circuit image, but rather to a general home page for the site. The site probably requires a login in order to proceed to the materials. You might want to cut the image out or redraw it and upload it here instead.

Even without seeing the circuit in question I can tell that this problem will be more suitable in the Introductory Physics forum, so I am moving it there.

 

[NascentOxygen]

We do get a glimpse of the page here. The background can be scrolled up & down & all revealed.

http://www.meritnation.com/cbse/cla...-shows-apotentiometer-circuit-for-comparison[

OP messed up the tags.

 

[gneill]

Okay, I grabbed a "snippy" of the image to take a look at the circuit. I don't see how the circuit can function as a bridge since one leg of the Galvanometer appears to have a fixed potential w.r.t. node A set by cell ε regardless of the values of resistors R and X. Also, I don't recognize the components shown as facing arcs in series with the resistors. Some "local dialect" version of a capacitor? Or perhaps they are push button switches to select one or the other resistor?

Also, the problem statement doesn't specify the total length of the resistive wire AB, so what are we to make of the measured values? Are we to assume that the length AB is 1 meter?

Overall I'm not impressed by the quality of Question 3.23.

 

[DEvens]

If I understand the picture correctly (after another poster gave a corrected link) it looks like R and X are parallel.

Under what circumstances could the current through parallel resistors be equal? Hint: How does the voltage across R compare to the voltage across X?

What does the balance point being given in cm mean? What does a potentiometer look like? Hint: Google images for "linear potentiometer."

 

[Prashasti]

They are keys. And the length of the wire is 1 metre. They aren't connected in parallel. We have to calculate the resistance of R and X using the device. When we switch the upper key on, we get a balance point at 58.3 cm and when we switch the lower key on, we get the balance point at 68.5 cm.
Sorry for that wrong link,

 

[gneill]

They are keys. And the length of the wire is 1 metre. They aren't connected in parallel. We have to calculate the resistance of R and X using the device. When we switch the upper key on, we get a balance point at 58.3 cm and when we switch the lower key on, we get the balance point at 68.5 cm.
Sorry for that wrong link,

So the "keys" are switches. Fine. But I don't see how the circuit can function as desired. The voltage source ε places a fixed potential at the lower end of galvanometer G (with respect to node A) regardless of which resistor is switched into the circuit.

 

[NascentOxygen]

Q3.24 on that site is illuminating, and suggests that Q3.23 should not be taken in isolation.

Q3.24 speaks of the internal resistance of the ε volts cell, and so it seems this should feature on the circuit at the centre of this thread!

All clear now! [PLAIN]http://imageshack.com/a/img29/6853/xn4n.gif [PLAIN]http://imageshack.com/a/img29/6853/xn4n.gif

 

[gneill]

Q3.24 on that site is illuminating, and suggests that Q3.23 should not be taken in isolation.

Q3.24 speaks of the internal resistance of the ε volts cell, and so it seems this should feature on the circuit at the centre of this thread!

All clear now! [PLAIN]http://imageshack.com/a/img29/6853/xn4n.gif [PLAIN]http://imageshack.com/a/img29/6853/xn4n.gif

Yes, well, I applaud your tenacity and extra effort
Given this new information the problem becomes solvable.

Here's a new depiction of the circuit. I've replaced the "keys" with an SPDT switch to make the selection operation clear, and made visible the internal resistance of the cell ε. We should wait for the OP to comment, see if he can offer an attempt at a solution.

 

[issacnewton]

I am also interested in this problem. So when the balance point is reached for $R = 10 \;\Omega$, I think there is no current flowing through the galvanometer. But can there be current through $\varepsilon$, $R$ and $r$ ?

 

[cnh1995]

But can there be current through εε\varepsilon, RRR and rrr ?

There is a current flowing through r, R and E. The circuit is closed.

 

[issacnewton]

Thanks cnh. Now let $i_1$ be the current through $R$ when the galvanometer is balanced. So the potential drop across $R$ would be $\frac{\varepsilon R}{R+r}$. Now when $X$ is connected instead of $R$, the potential drop across $X$ would $\frac{\varepsilon X}{X+r}$ These two potentials are related to the respective balance points
$$\frac{\varepsilon R}{R+r} = k(58.3)$$
$$\frac{\varepsilon X}{X+r} = k (68.5)$$
where $k$ is the proportionality constant between the resistance and the length. Now dividing one equation by the other, we get
$$\left(\frac{\varepsilon R}{R+r} \right) \left( \frac{X+r}{\varepsilon X} \right) = \frac{58.3}{68.5} $$
which leads to
$$\left(\frac{R}{R+r} \right) \left( \frac{X+r}{X} \right) = \frac{58.3}{68.5} $$
Now here both $X$ and $r$ are unknown. So how can we solve for $X$ ?

 

[cnh1995]

So how can we solve for XXX ?

Given the circuit in #9, I believe we can't.
We can solve for X only I) if the ideal battery voltage V_AB is known
OR
II) if we are allowed to use one more known resistance.

In I), we would first need to find the emf of the lower cell (by discarding the switch-resistance arrangement and finding null point) and then we can find the internal resistance of the same cell using known resistance . Once you know ε and r, you can solve for X given its balancing length. (Sounds very tedious!).

In II)You can set up two equations with two known resistances and find r. Then use the last equation in #12 to find X.

 

[issacnewton]

As it stands, no additional information is given so this problem can not be solved. This is a problem from NCERT Physics book. Lot of problems in that book have confusing language. I doubt if authors themselves know the basic physics.

 

[cnh1995]

Lot of problems in that book have confusing language

I agree.
The transistor-amplifier part in that book is also flawed, with incorrect circuit diagram and handwavy explanations contradicting circuit theory.
https://www.physicsforums.com/threads/input-signal-in-a-transistor.918672/

The book really needs some serious reviewing.