barvas11
- 32
- 0
Hi Guys,
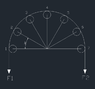
I have a sheave with 7 rollers spread evenly on 180° radius. There is an equal amount of force on each end of the sheave pulling down.
My question is will the force acting on rollers be the same for all rollers or will it differ depending on the angle?
I have attached the picture for better illustration.
Thanks for your advice
I have a sheave with 7 rollers spread evenly on 180° radius. There is an equal amount of force on each end of the sheave pulling down.
My question is will the force acting on rollers be the same for all rollers or will it differ depending on the angle?
I have attached the picture for better illustration.
Thanks for your advice