oooobs
- 2
- 0
hey I am 16, grade 12 in australia, struggling on the hardest question on the current maths assignment.
i was wondering if someone could point me in the right direction?
i really have no idea where to start. and no one i seem to ask has any useful info.
Background knowledge:
In a very simplified SAI allocation system, the top student is awarded 400, the bottom student is awarded 200 and the remainder of the cohort is given a whole number score beetween these values (reflecting their position in the cohort).
Across the state, OP's (overall positions) are awarded according to the following approximate percentage breakdown. the top 2% of students receive an OP of 1; the next 19% receive an OP 2-6; the next 73% receive an OP 7-21; the next 5% receive an OP 22-24; and the final 1% receive an OP 25.
QUESTION IS AS FOLLOWS:
Consider a cohort of 15 students. investigate possible SAI allocations with the gloal of achieving the best possible OP results for your cohort.
Normal Distribution Formula :
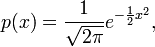
Comments:
i don't expect anyone to give me the answer i just want to be pointed in the right direction
thanks in advance!
~Dru Arnfield
i was wondering if someone could point me in the right direction?
i really have no idea where to start. and no one i seem to ask has any useful info.
Homework Statement
Background knowledge:
In a very simplified SAI allocation system, the top student is awarded 400, the bottom student is awarded 200 and the remainder of the cohort is given a whole number score beetween these values (reflecting their position in the cohort).
Across the state, OP's (overall positions) are awarded according to the following approximate percentage breakdown. the top 2% of students receive an OP of 1; the next 19% receive an OP 2-6; the next 73% receive an OP 7-21; the next 5% receive an OP 22-24; and the final 1% receive an OP 25.
QUESTION IS AS FOLLOWS:
Consider a cohort of 15 students. investigate possible SAI allocations with the gloal of achieving the best possible OP results for your cohort.
Homework Equations
Normal Distribution Formula :
Comments:
i don't expect anyone to give me the answer i just want to be pointed in the right direction
thanks in advance!
~Dru Arnfield