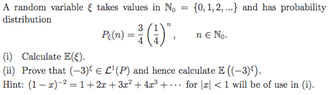The discussion revolves around calculating expected values using a discrete probability distribution function, specifically P{ξ = n} = (3/4)(1/4)^n. Participants clarify the application of the series sum for expected value calculations, leading to E{ξ} = 1/3 and E{(-3)ξ} = 3/7. Confusion arises regarding the coefficients in the series, particularly whether to use 3/4 or 1/4 in the calculations. After addressing the misunderstanding, the correct approach is confirmed, and gratitude is expressed for the assistance. The thread highlights the importance of careful application of series in probability calculations.