Problem involving a definite integral

[ubergewehr273]

Homework Statement

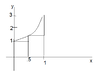
Refer the image.

Homework Equations

Integral (e^x)dx from 0 to 1=e-1.

The Attempt at a Solution

Refer the other image. The graph of e^(x^2) increases more slowly than e^x till x=1.
So 'a' is clearly greater than 1. Is this right?

 

[Mark44]

Thread moved. Please post problems involving integrals in the Calculus & Beyond section, not in the Precalculus section.

The graph of e^(x^2) increases more slowly than e^x till x=1.

What does $e^x$ have to do with anything? The integrand is $e^{x^2}$.

 

[ubergewehr273]

What does $e^x$ have to do with anything? The integrand is $e^{x^2}$.

So that $\int_0^1 e^{x^2}\,dx$ and $\int_0^1 e^x\,dx$ can be compared.
Clearly $\int_0^1 e^{x^2}\,dx$ < $\int_0^1 e^x\,dx$

 

[Mark44]

So that $\int_0^1 e^{x^2}\,dx$ and $\int_0^1 e^x\,dx$ can be compared.
Clearly $\int_0^1 e^{x^2}\,dx$ < $\int_0^1 e^x\,dx$

Sure, they can be compared.
Relative to this problem, you have $e - 1 = a\int_0^1 e^{x^2}dx < a\int_0^1 e^x dx =$?
Can you fill in for the question mark?
What does this say about a?
Do you still believe that a > 1?

 

[ubergewehr273]

So that $\int_0^1 e^{x^2}\,dx$ and $\int_0^1 e^x\,dx$ can be compared.
Clearly $\int_0^1 e^{x^2}\,dx$ < $\int_0^1 e^x\,dx$

$a=\frac{e-1} {\int_0^1 e^{x^2}\,dx}$
And from the above quoted equation,
$a=\frac{e-1} {<e-1}$
Hence $a>1$. Is this correct?

 

[Mark44]

$a=\frac{e-1} {\int_0^1 e^{x^2}\,dx}$
And from the above quoted equation,
$a=\frac{e-1} {<e-1}$
Hence $a>1$. Is this correct?

Yes.

 

[ubergewehr273]

Yes.

Then from there on how do I proceed? Options B and C get ruled out.

 

[Mark44]

You have an upper bound on $\int_0^1 e^{x^2}dx$, namely $\int_0^1 e^x = e - 1$, so now you need a lower bound on that integral.
What about a Riemann sum? You could get a lower bound by dividing the interval [0, 1] into two parts, and calculating the areas of the two rectangular areas under the graph of $y = e^{x^2}$.

Here's what I have in mind -- it's a pretty crude sketch, but maybe it gets my idea across. The curve is supposed to be the graph of $y = e^{x^2}$.