Problem involving Torque and a Derrick from Feynman Exercises

In summary, the conversation discussed the attempt to solve a problem involving the torque caused by tension and weight on a derrick. The principle of virtual work was also used to arrive at the same answer. The questioner was unsure about the presence of an additional term in the listed answer and sought clarification.
  • #1
suh112
4
4
Homework Statement
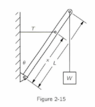
2.17 A derrick is made of a uniform boom of length L and weight w, pivoted at its lower end, as shown in Fig. 2-15. It is supported at an angle with the vertical by a horizontal cable attached at a point a distance x from the pivot, and a weight W is slung from its upper end. Find the tension T in the horizontal cable.
Relevant Equations
##\tau = F_{\perp}r##
Work = Fd
I attempted to solve this problem by considering the torque caused by the perpendicular components of the tension and weight with respect to the derrick. $$ Tcos\theta x = Wsin\theta L$$ $$T = \frac L x Wtan\theta$$ Using the principle of virtual work I also arrived at the same answer by considering the derrick falling a distance y. $$Wsin\theta y = Tcos\theta \frac x L y $$The answer listed in the book is ##T = \frac L x (W + \frac W 2 )tan\theta ## and I can't figure out where the ##\frac W 2 ## term comes from. Thank you in advance for helping me.
 

Attachments

  • Screen Shot 2023-01-04 at 11.45.41 AM.png
    Screen Shot 2023-01-04 at 11.45.41 AM.png
    22 KB · Views: 71
Physics news on Phys.org
  • #2
In addition to the weight W of the block, the boom has weight w.
 
  • #3
TSny said:
In addition to the weight W of the block, the boom has weight w.
Ok I see now. Thanks for pointing that out.
 
  • Like
Likes berkeman and TSny

FAQ: Problem involving Torque and a Derrick from Feynman Exercises

What is torque in the context of a derrick problem?

Torque, in the context of a derrick problem, refers to the rotational force applied to the derrick's arm or boom. It is calculated as the product of the force applied and the perpendicular distance from the pivot point (usually the base of the derrick) to the line of action of the force.

How do you calculate the torque produced by a force in a derrick system?

To calculate the torque produced by a force in a derrick system, you use the formula: Torque (τ) = Force (F) × Lever Arm Distance (r) × sin(θ), where θ is the angle between the force vector and the lever arm. If the force is perpendicular to the lever arm, the sine component becomes 1, simplifying the formula to τ = F × r.

What role does the angle of the derrick arm play in solving torque problems?

The angle of the derrick arm is crucial in solving torque problems because it affects the effective lever arm distance. The torque is maximized when the force is applied perpendicular to the arm. If the force is applied at an angle, the effective distance is reduced by the cosine of the angle between the force direction and the arm.

How do you determine the equilibrium condition for a derrick under multiple forces?

To determine the equilibrium condition for a derrick under multiple forces, you need to ensure that the sum of all torques around the pivot point is zero and that the sum of all forces in both the horizontal and vertical directions is zero. Mathematically, this means Στ = 0, ΣF_x = 0, and ΣF_y = 0.

What are common mistakes to avoid when solving torque problems involving a derrick?

Common mistakes to avoid include not properly accounting for the direction of the forces and their respective angles, neglecting the weight of the derrick arm itself, assuming all forces act perpendicular to the arm, and forgetting to include the torque due to the derrick's own weight. Ensuring all units are consistent and double-checking calculations can help prevent these errors.

Similar threads

Frequency & Wavelength of a Vibrating Wire
Replies
5
Views
964
Torque on a Circular Current Loop under a Misaligned Magnetic Field
Replies
1
Views
589
Two masses connected by Pulley - Lagrangian problem
Replies
6
Views
543
Tangential velocity of rotating rod
Replies
5
Views
1K
Triangle problem from Feynman's exercises
Replies
5
Views
2K
Solving the Weight Puzzle: Explaining Why and How
Replies
2
Views
1K
The leaning ladder problem using Newtonian mechanics
Replies
27
Views
3K
Why Does Virtual Work Seem Incorrect in This Statics Problem?
Replies
12
Views
2K
Tension in a deformed cylindrical bag on a surface
Replies
18
Views
829
Force Acting on Hinge: 2744 N Torque on Beam Homework: Find Force on Hinge
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top