- #1
asynja
- 16
- 0
Hello! I have a problem in classical mechanics that I'm unable to solve. Any help would be much appreciated since we have a partial exam tomorrow. :(
There's a picture of the problem in the attachment
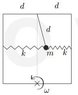
A mass m, which is on a light rod (lenght d), is attached to a square frame with sides 2d and to two springs with coefficient k, as shown on the picture. The length of unstreched springs is d. We put the frame on the surface and spin it around the point s with angular speed ω. We assume that there is no friction between mass and the surface and that springs can slide up and down the frame (they are not fixated).
Find the Lagrange function and the equation of motion for the mass.
Where are the stationary positions? For which coefficients k is the stationary position stable when the springs are the least streched?
Lagrange's formalism
T=1/2mω2 , V=kx2*2 , but then I don't know how to take into the account the effect that rod with length d has on the springs (it contributes that they are stretched more, right?)
Homework Statement
There's a picture of the problem in the attachment
A mass m, which is on a light rod (lenght d), is attached to a square frame with sides 2d and to two springs with coefficient k, as shown on the picture. The length of unstreched springs is d. We put the frame on the surface and spin it around the point s with angular speed ω. We assume that there is no friction between mass and the surface and that springs can slide up and down the frame (they are not fixated).
Find the Lagrange function and the equation of motion for the mass.
Where are the stationary positions? For which coefficients k is the stationary position stable when the springs are the least streched?
Homework Equations
Lagrange's formalism
The Attempt at a Solution
T=1/2mω2 , V=kx2*2 , but then I don't know how to take into the account the effect that rod with length d has on the springs (it contributes that they are stretched more, right?)