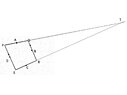
SUMMARY
The forum discussion focuses on proving that quadrilateral ABCD is a parallelogram using properties of triangles and midsegments. The user initially struggles with the relationship between segments AD and QS, ultimately concluding that AD is equal to half of QS and parallel to it, as per the triangle midsegment theorem. The discussion emphasizes that both pairs of opposite sides being parallel and equal in length are essential criteria for establishing ABCD as a parallelogram. Additionally, the similarity of triangles PST and QRT is established through corresponding angles and side ratios.
PREREQUISITES
- Understanding of triangle properties, specifically the triangle midsegment theorem.
- Knowledge of parallel lines and corresponding angles.
- Familiarity with the definitions of parallelograms and similar triangles.
- Basic skills in geometric proofs and reasoning.
NEXT STEPS
- Study the triangle midsegment theorem in detail.
- Learn how to prove properties of parallelograms using parallel lines.
- Explore the concept of similar triangles and their applications in proofs.
- Practice geometric proof techniques with various quadrilaterals.
USEFUL FOR
Students studying geometry, educators teaching geometric proofs, and anyone seeking to understand properties of parallelograms and triangle similarity.