- #1
Jhenrique
- 685
- 4
If work ##W = \Delta E = \int_{s} \vec{F} \cdot d\vec{s}##, so work can't be ##\frac{dW}{d\vec{s}} = \vec{F}## like is here: http://en.wikipedia.org/wiki/Work_(physics)#Path_dependence
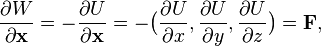
cause this implies that ##W = \int \vec{F} \cdot d\vec{s} = E##, but the work is the variation of the energy, and not the energy.
Again, the impulse ##\vec{J} = \Delta \vec{p}##, if I says that ##\frac{d\vec{J}}{dt} = \vec{F}##, this implies that the impulse ##\vec{J} = \int \vec{F} dt = \vec{p}##, but the impulse is the variation of the momentum and not the momentum.
So, how can I administer these operations of a coherent way?
cause this implies that ##W = \int \vec{F} \cdot d\vec{s} = E##, but the work is the variation of the energy, and not the energy.
Again, the impulse ##\vec{J} = \Delta \vec{p}##, if I says that ##\frac{d\vec{J}}{dt} = \vec{F}##, this implies that the impulse ##\vec{J} = \int \vec{F} dt = \vec{p}##, but the impulse is the variation of the momentum and not the momentum.
So, how can I administer these operations of a coherent way?