Product Rule with Partial Derivatives

[Vapor88]

Hi, so I'm trying to solve Laplace's equation by separation of variables, and there's a basic step I'm not understanding with regards to the product rule.

Given

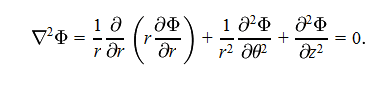
A product rule (i think) is taken to make the first term easier to deal with and we get

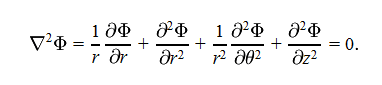
I'm just having trouble understanding what the derivatives of f and g are. And am I correct in saying that f = 1/r*partial wrt r
g = r * partial phi wrt r

Thank you

 

[gabbagabbahey]

I'm just having trouble understanding what the derivatives of f and g are. And am I correct in saying that f = 1/r*partial wrt r
g = r * partial phi wrt r

No, to apply the product rule to \frac{\partial}{\partial r}\left(r\frac{\partial \Phi}{\partial r}\right), you let f(r)=r and g(r)=\frac{\partial \Phi}{\partial r}.

 

[Vapor88]

If that's the case, then I have a problem. How do you multiply partial derivatives together? I don't see at all how you go from equation one to equation two.

 

[Coto]

Hey Vapor,

If you are trying to use separation of variables then your first step should be:
\phi = f(r)g(\theta)h(z).

Coto

 

[Vapor88]

Coto,

I'm okay on that end of things, and understand every step when I plug those equations in, but I just can't get a grasp of this first one.

 

[Coto]

Hmm :). Generally speaking, it doesn't make sense to separate that derivative. It makes more sense to keep it as is since you can then easily solve the differential equation that results for r.

In other words, applying the product rule actually moves you back a step!

Anyway, the product rule is:
\frac{d}{dr}(f(r) \cdot g(r)) = g(r)\frac{df}{dr} + f(r)\frac{dg}{dr}.

Use this in combination with gabbas advice, where,
\frac{d}{dr}\frac{d\phi}{dr} = \frac{d^2\phi}{dr^2}.

 

[gabbagabbahey]

As coto says, the product rule tells you that

\frac{\partial}{\partial r}\left(r\frac{\partial \Phi}{\partial r}\right)=\frac{\partial}{\partial r}\left(f(r)g(r)\right)=\frac{\partial f}{\partial r}g(r)+f\frac{\partial g}{\partial r}

So, calculate \frac{\partial f}{\partial r}[/itex] and \frac{\partial g}{\partial r}[/itex] and see what that gives you.

 

[gabbagabbahey]

Hmm :). Generally speaking, it doesn't make sense to separate that derivative. It makes more sense to keep it as is since you can then easily solve the differential equation that results for r.

That depends on what form you are used to seeing Bessel's differential equation in.

 

[Coto]

That depends on what form you are used to seeing Bessel's differential equation in.

I suppose. I strongly encourage the "Sturm-Liouville" form.

 

[Vapor88]

Excellent. I now understand. I guess I was just having a problem with the notation of it. I didn't understand that the partial wrt r was for what was in the parentheses after it, and that the 1/r term is simply multiplied through afterwards. Thanks!